题目内容
a，b均为有理数，下列判断：
①a2+（b+1）2总是正数；②a2+b2+1总是正数；③9+（a-b）2的最小值是9；④1-（1+ab）2的最大值是1．
其中正确的个数有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析：根据平方数非负数的性质，对各小题举例判断即可得解．
解答：①a2+（b+1）2，当a=0，b=-1时，结果等于0，故本小题错误；
②∵a2≥0，b2≥0，∴a2+b2+1≥1，总是正数，故本小题正确；
③∵（a-b）2≥0，∴9+（a-b）2最小值是9，故本小题正确；
④∵（1+ab）2≥0，∴-（1+ab）2≤0，∴1-（1+ab）2的最大值是1，故本小题正确．
所以正确的有②③④共3个．
故选C．
点评：本题考查了平方数非负数的性质，通过举例分析是解题的关键．
分析：根据平方数非负数的性质，对各小题举例判断即可得解．
解答：①a2+（b+1）2，当a=0，b=-1时，结果等于0，故本小题错误；
②∵a2≥0，b2≥0，∴a2+b2+1≥1，总是正数，故本小题正确；
③∵（a-b）2≥0，∴9+（a-b）2最小值是9，故本小题正确；
④∵（1+ab）2≥0，∴-（1+ab）2≤0，∴1-（1+ab）2的最大值是1，故本小题正确．
所以正确的有②③④共3个．
故选C．
点评：本题考查了平方数非负数的性质，通过举例分析是解题的关键．
练习册系列答案
相关题目
、B=
（a，b，m均为有理数）都是无理数，满足：①A+B=2a为有理数，②AB=a2-mb2为有理数．称A、B两数为一对共轭数．（如：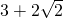
，
，∵
=
，∴
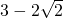，B=a-b
，3-2
、3-2
，-
，-2，3．现将这4张卡片洗匀后正面向下放在桌子上，