题目内容
【题目】(1)(3分)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD∶GC∶EB的结果(不必写计算过程);
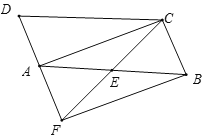
(2)(3分)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD∶GC∶EB;
(3)(2分)把图(2)中的正方形都换成矩形,如图(3),且已知DA∶AB=HA∶AE=m: n,此时HD∶GC∶EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).

【答案】(1)HD:GC:EB=1:![]() :1(2)HD:GC:EB=1:
:1(2)HD:GC:EB=1: ![]() :1(3)有变化,HD:GC:EB=
:1(3)有变化,HD:GC:EB=![]()
【解析】解:(1)HD:GC:EB=1:![]() :1。
:1。
(2)连接AG、AC,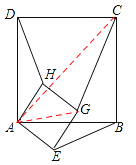
∵△ADC和△AHG都是等腰直角三角形,
∴AD:AC=AH:AG=1: ![]() ,∠DAC=∠HAG=45°。
,∠DAC=∠HAG=45°。
∴∠DAH=∠CAG。∴△DAH∽△CAG。
∴HD:GC=AD:AC=1: ![]() 。
。
∵∠DAB=∠HAE=90°,∴∠DAH=∠BAE。
又∵AD=AB,AH=AE,∴△DAH≌△BAE(SAS)。∴HD=EB。
∴HD:GC:EB=1: ![]() :1。
:1。
(3)有变化,HD:GC:EB=![]() 。
。
(1)连接AG,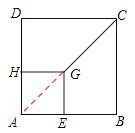
∵正方形AEGH的顶点E、H在正方形ABCD的边上,
∴∠GAE=∠CAB=45°,AE=AH,AB=AD。
∴A,G,C共线,AB-AE=AD-AH,∴HD=BE。
∵![]()
∴GC=AC-AG=![]() AB-
AB-![]() AE=
AE= ![]() (AB-AE)=
(AB-AE)= ![]() BE。
BE。
∴HD:GC:EB=1:![]() :1。
:1。
(2)连接AG、AC,由△ADC和△AHG都是等腰直角三角形,易证得△DAH∽△CAG与△DAH≌△BAE,利用相似三角形的对应边成比例与正方形的性质,即可求得HD:GC:EB的值。
(3)连接AG、AC,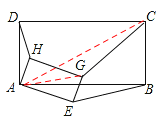
∵矩形AEGH的顶点E、H在矩形ABCD的边上,
DA:AB=HA:AE=m:n,
∴∠ADC=∠AHG=90°,∴△ADC∽△AHG。
∴AD:AC=AH:AG=![]() ,∠DAC=∠HAG。
,∠DAC=∠HAG。
∴∠DAH=∠CAG。∴△DAH∽△CAG。
∴HD:GC=AD:AC=![]() 。
。
∵∠DAB=∠HAE=90°,∴∠DAH=∠BAE。
∵DA:AB=HA:AE=m:n,∴△ADH∽△ABE。∴DH:BE=AD:AB=m:n。
∴HD:GC:EB=![]() 。
。

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案