题目内容
(2011•恩施州)如图,在平面直角坐标系中,直线AC: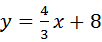 与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A、点C,且与x轴的另一交点为B(x0,0),其中x0>0,又点P是抛物线的对称轴l上一动点.
与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A、点C,且与x轴的另一交点为B(x0,0),其中x0>0,又点P是抛物线的对称轴l上一动点.
(1)求点A的坐标,并在图1中的l上找一点P0,使P0到点A与点C的距离之和最小;
(2)若△PAC周长的最小值为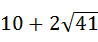 ,求抛物线的解析式及顶点N的坐标;
,求抛物线的解析式及顶点N的坐标;
(3)如图2,在线段CO上有一动点M以每秒2个单位的速度从点C向点O移动(M不与端点C、O重合),过点M作MH∥CB交x轴于点H,设M移动的时间为t秒,试把△P0HM的面积S表示成时间t的函数,当t为何值时,S有最大值,并求出最大值;
(4)在(3)的条件下,当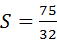 时,过M作x轴的平行线交抛物线于E、F两点,问:
时,过M作x轴的平行线交抛物线于E、F两点,问:
过E、F、C三点的圆与直线CN能否相切于点C?请证明你的结论.(备用图图3)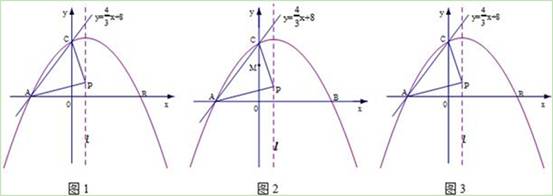
解:(1)由题意直线AC与x轴的交点,
所以当y=0,则x=﹣6,
所以点A(﹣6,0).
同理点C(0,8),
设点A关于y轴对称点为B(x′,0),
由题意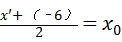 则x′=2x0+6.
则x′=2x0+6.
则直线BC为y=﹣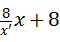 ,
,
代入x=x0,则y=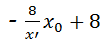 ,
,
所以该点为(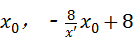 ),
),
即(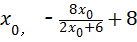 );
);
(2)由(1)可知三角形PAC最小即为AC+BC=10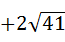 ,
,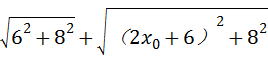 =10
=10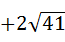 ,
,
解得x0=2或x0=﹣8(不符舍去),
则点B(10,0),
由点A,B,C三点的二次函数式为y= .
.
点N(2,16);
(3)如图,作MN⊥BC与N,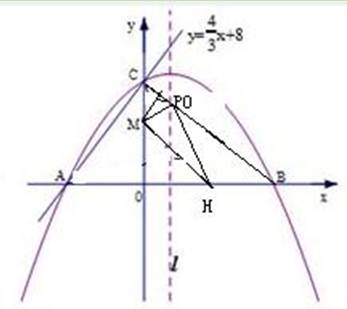
则在三角形OBC∽三角形CMN,
所以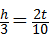 ,
,
即h=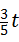 .
.
因为MH∥BC,
所以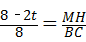 ,
,
解得MH=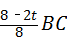 =
=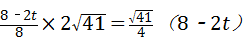 ,
,
S=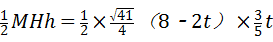 =
=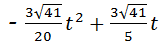 ,
,
因为每秒移动2个单位,
则当t=2时符合范围0<t<4,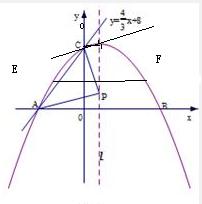
所以当t为2时S最大;
(4)把S的取值代入(3)中表达式中求得t,
从而得到点M的坐标,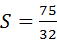 ,即
,即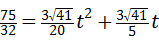
则解得t=2,
则由题意知CEF三点所在圆半径为4,
所以直线CN与CFE所在圆相切.
解析

 阅读快车系列答案
阅读快车系列答案| A.a6÷a2=a3 | B.a5﹣a3=a2 |
| C.(3a3)2=6a9 | D.2(a3b)2﹣3(a3b)2=﹣a6b2 |
(2011•恩施州)宜万铁路开通后,给恩施州带来了很大方便.恩施某工厂拟用一节容积是90立方米、最大载重量为50吨的火车皮运输购进的A、B两种材料共50箱.已知A种材料一箱的体积是1.8立方米、重量是0.4吨;B种材料一箱的体积是1立方米、重量是1.2吨;不计箱子之间的空隙,设A种材料进了x箱.
(1)求厂家共有多少种进货方案(不要求列举方案)?
(2)若工厂用这两种材料生产出来的产品的总利润y(万元)与x(箱)的函数关系大致如下表,请先根据下表画出简图,猜想函数类型,求出函数解析式(求函数解析式不取近似值),确定采用哪种进货方案能让厂家获得最大利润,并求出最大利润.
| x | 15 | 20 | 25 | 30 | 38 | 40 | 45 | 50 |
| y | 10 | 约27.58 | 40 | 约48.20 | 约49.10 | 约47.12 | 40 | 约26.99 |

 )÷
)÷ •
• ,再从﹣3、
,再从﹣3、 ﹣3、2、﹣2中选一个你喜欢的数作为a的值代入求值.
﹣3、2、﹣2中选一个你喜欢的数作为a的值代入求值. 和x轴上,则第n个阴影正方形的面积为
和x轴上,则第n个阴影正方形的面积为 