Question

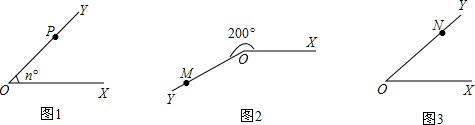
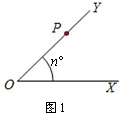
如图1，将射线OX绕点O按逆时针旋转n°的角，得到射线OY，如果点P为射线OY上一点，且OP＝a，那么我们就规定用(a，n°)表示点P在平面内的位置，并记为P(a，n°)．例如在图2中，如果OM＝6，∠XOM＝200°，那么点M在平面内的位置记为M(6，200°)．

 

根据上述规定解答下列问题：

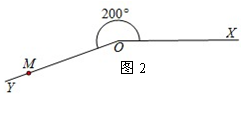
（1）在图3中，如果点N在平面内的位置记为N(10，35°)，那么ON＝____，∠XON＝____°；

（2）将图3中的射线OY绕点O旋转一定的角度（小于360度），使得旋转后所得到的射线OZ与射线OY垂直，则旋转后点N在平面内的位置可记为_______          _，请在图3中画出旋转后的图形．

 

Answer 1

【答案】

（1）10、35°；（2）N（10，125°）或（10，305°），如图所示：

【解析】

试题分析：（1）根据题目中的定义，第一个坐标表示点到O的距离，第二个表示角度，据此即可直接回答；

（2）结合（1）的结论和旋转的性质，知ON=6，∠XOY′=90°+30°=120°．

（1）根据定义得ON=10，∠XON=35°；

（2）如图所示，根据旋转的性质，得ON的长不变，∠XOY′=90°+35°=1205°．

则点N旋转后在平面内的位置记为（10，125°）或（10，306°），如图所示：

考点：旋转的性质

点评：解题的关键是读懂题意，正确理解新定义，同时熟练掌握旋转对应边的夹角是旋转角.