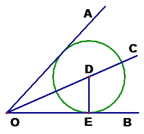
题目内容
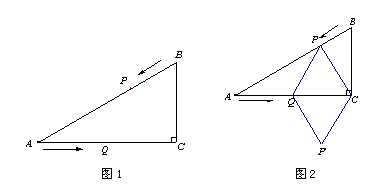
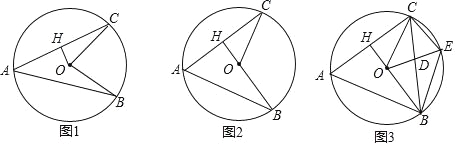
【题目】如图,点![]() 是线段
是线段![]() 的中点,分别以
的中点,分别以![]() 为边作等腰
为边作等腰![]() 和等腰
和等腰![]() ,
,![]() ,连接
,连接![]() ,且
,且![]() 相交于点
相交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则下列说法中,不正确的是( )
,则下列说法中,不正确的是( )

A.![]() 是
是![]() 的中线B.四边形
的中线B.四边形![]() 是平行四边形
是平行四边形
C.![]() D.
D.![]() 平分
平分![]()
【答案】D
【解析】
根据平行四边形、全等三角形的判定与性质以及等腰三角形三线合一的性质,逐一判定即可.
∵点![]() 是线段
是线段![]() 的中点,
的中点,
∴BC=EC
∵等腰![]() 和等腰
和等腰![]() ,
,![]() ,
,
∴AB=AC=CD=DE,∠ABC=∠ACB=∠DCE=∠DEC=45°
∴∠ACD=90°,AD=BC=EC
∴∠CAD=∠CDA=45°
∴AD∥BE
∴四边形![]() 是平行四边形,故B选项正确;
是平行四边形,故B选项正确;
在△ABE和△DEB中,

∴△ABE≌△DEB(SAS)
∴![]() ,故C选项正确;
,故C选项正确;
∴∠DBE=∠AEB
∴FC⊥BE
∵AD∥BE
∴FC⊥AD
∴![]() 是
是![]() 的中线,故A选项正确;
的中线,故A选项正确;
∵AC≠CE
∴![]() 不可能平分
不可能平分![]() ,故D选项错误;
,故D选项错误;
故选:D.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目