题目内容
在△ABC中,∠C=90°,a、b分别是∠A、∠B所对的两条直角边,c是斜边,则有
A. sinA=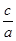 B. cosB=
B. cosB=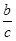 C. tanA=
C. tanA= D. cosB=
D. cosB=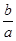
A. sinA=
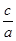 B. cosB=
B. cosB=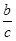 C. tanA=
C. tanA= D. cosB=
D. cosB=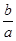
C
根据锐角三角函数的定义解答即可.
解:∵在△ABC中,∠C=90°,a,b分别是∠A,∠B所对的两条直角边,c是斜边,
∴sinA= ,cosB=
,cosB= ,tanA=
,tanA= ,cotB=
,cotB= .
.
故选C.
本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,余切等于邻边比对边.
解:∵在△ABC中,∠C=90°,a,b分别是∠A,∠B所对的两条直角边,c是斜边,
∴sinA=
 ,cosB=
,cosB= ,tanA=
,tanA= ,cotB=
,cotB= .
.故选C.
本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,余切等于邻边比对边.

练习册系列答案
相关题目

 y
y 与-x
与-x y
y 是同类项,则m="_____," n=_______;
是同类项,则m="_____," n=_______;

 为
为 ,弦AB的长为
,弦AB的长为 cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为
cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为
 cm
cm cm
cm cm
cm cm
cm 向上平移2个单位,所得直线表达式是______
向上平移2个单位,所得直线表达式是______



