题目内容
如图，扇形纸片的圆心角
为
，弦AB的长为
cm，用它围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为
为，弦AB的长为cm，用它围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为A． cm | B． cm | C． cm | D． cm |
A
分析：因为圆锥的高，底面半径，母线构成直角三角形．先求出扇形的半径，再求扇形的弧长，利用扇形的弧长等于圆锥底面周长作为相等关系求底面半径．
解答：解：设扇形OAB的半径为R，底面圆的半径为r
则R2=（
）2+(
)2
解得R=2cm
∴扇形的弧长=
=2πr
解得，r=
cm
故选A．
解答：解：设扇形OAB的半径为R，底面圆的半径为r
则R2=（
）2+()2解得R=2cm
∴扇形的弧长=
=2πr解得，r=
cm故选A．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
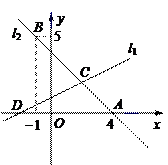
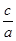B. cosB=
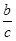C. tanA=
D. cosB=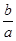
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
的值为（ ▼ ）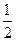
，∠A的正对值sad A的取值范围是 ▼ .
，其中
为锐角，试求sad
，△ABC是 【 】