题目内容
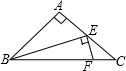 如图,在等腰直角三角形ABC中,AB=1,∠A=90°,点E为腰AC的中点,点F在底边BC上,且FE⊥BE,求△CEF的面积.
如图,在等腰直角三角形ABC中,AB=1,∠A=90°,点E为腰AC的中点,点F在底边BC上,且FE⊥BE,求△CEF的面积.
解法1:如图,过C作CD⊥CE与EF的延长线交于D.
因为∠ABE+∠AEB=90°,∠CED+∠AEB=90°,所以∠ABE=∠CED.
于是Rt△ABE∽Rt△CED,
所以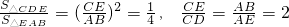 .()
.()
又∠ECF=∠DCF=45°,所以CF是∠DCE的平分线,点F到CE和CD的距离相等,
所以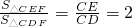 .
.
所以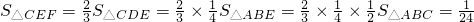 .
.
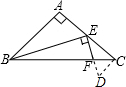
解法2:如图,作FH⊥CE于H,设FH=h.因为∠ABE+∠AEB=90°,∠FEH+∠AEB=90°,所以∠ABE=∠FEH,
于是Rt△EHF∽Rt△BAE.
因为 ,所以
,所以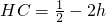 .
.
又因为HC=FH,所以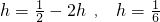 ,
,
所以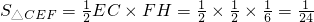 .
.
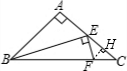
分析:过C作CD⊥CE与EF的延长线交于D,构成直角三角形可证出Rt△ABE∽Rt△CED,然后证出其面积;或作FH⊥CE于H,设FH=h,Rt△EHF∽Rt△BAE,然后求出其面积.
点评:本题的关键是作出辅助线,然后构成直角三角形,用相似三角形的性质求面积.
因为∠ABE+∠AEB=90°,∠CED+∠AEB=90°,所以∠ABE=∠CED.
于是Rt△ABE∽Rt△CED,
所以
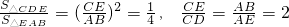 .()
.()又∠ECF=∠DCF=45°,所以CF是∠DCE的平分线,点F到CE和CD的距离相等,
所以
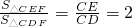 .
.所以
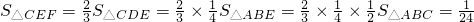 .
.
解法2:如图,作FH⊥CE于H,设FH=h.因为∠ABE+∠AEB=90°,∠FEH+∠AEB=90°,所以∠ABE=∠FEH,
于是Rt△EHF∽Rt△BAE.
因为
 ,所以
,所以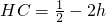 .
.又因为HC=FH,所以
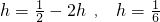 ,
,所以
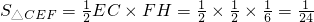 .
.
分析:过C作CD⊥CE与EF的延长线交于D,构成直角三角形可证出Rt△ABE∽Rt△CED,然后证出其面积;或作FH⊥CE于H,设FH=h,Rt△EHF∽Rt△BAE,然后求出其面积.
点评:本题的关键是作出辅助线,然后构成直角三角形,用相似三角形的性质求面积.

练习册系列答案
相关题目
教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:

(1)sad 的值为( ▼ )
的值为( ▼ )
(2)对于 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .
(3)已知 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A=
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:

(1)sad
 的值为( ▼ )
的值为( ▼ )A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad  的值为( ▼ )
的值为( ▼ )
A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 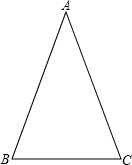 互唯一确定的.
互唯一确定的.
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
 的值为( ▼ )
的值为( ▼ ) B.
1 C.
B.
1 C.  D.
2
D.
2 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ . ,其中
,其中 为锐角,试求sad
为锐角,试求sad