题目内容
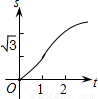
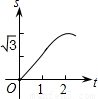
 如图,在直角坐标系的第一象限内,等边△ABO的边长为2,O为坐标原点,平行于y轴的动直线m沿OB方向平行移动,且与x轴相交于点D(x,0)(0≤x≤2),直线m截△ABO得直线m左侧的部分图形的面积y,那么y与x的函数关系图象大致是( )
如图,在直角坐标系的第一象限内,等边△ABO的边长为2,O为坐标原点,平行于y轴的动直线m沿OB方向平行移动,且与x轴相交于点D(x,0)(0≤x≤2),直线m截△ABO得直线m左侧的部分图形的面积y,那么y与x的函数关系图象大致是( )A、 | B、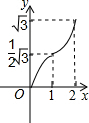 | C、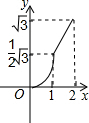 | D、 |
分析:根据等边△AOB中,l∥y轴,所以很容易求得∠OCB=30°;进而证明OD=x,CD=
x;最后根据三角形的面积公式,解答出S与x之间的函数关系式,由函数解析式来选择图象.
| 3 |
解答:解:①∵l∥y轴,△AOB为等边三角形,
∴∠OCB=30°,
∵点D(x,0),
∴OD=x,CD=
x;
∴S△OCD=
×OD×CD
=
x2(0≤x≤1),
即S=
x2(0≤x≤1).
∴S与x之间的函数关系的图象应为定义域为[0,1]、开口向上的二次函数图象;
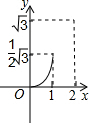
②∵l∥y轴,△AOB为等边三角形
∴∠CBD=30°,
∵点D(x,0),
∴BD=2-x,CD=
(2-x);
∴S△BCD=
×BD×CD
=
(2-x)2(1≤x≤2),
即S=
-
(2-x)2(1≤x≤2).
∴S与x之间的函数关系的图象应为定义域为[1,2],开口向下的二次函数图象.
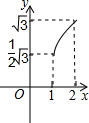
故选:A.
∴∠OCB=30°,
∵点D(x,0),
∴OD=x,CD=
| 3 |
∴S△OCD=
| 1 |
| 2 |
=
| ||
| 2 |
即S=
| ||
| 2 |
∴S与x之间的函数关系的图象应为定义域为[0,1]、开口向上的二次函数图象;

②∵l∥y轴,△AOB为等边三角形
∴∠CBD=30°,
∵点D(x,0),
∴BD=2-x,CD=
| 3 |
∴S△BCD=
| 1 |
| 2 |
=
| ||
| 2 |
即S=
| 3 |
| ||
| 2 |
∴S与x之间的函数关系的图象应为定义域为[1,2],开口向下的二次函数图象.
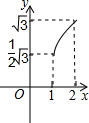
故选:A.
点评:此题主要考查的是二次函数解析式的求法及二次函数的图象特征,根据t的取值范围分别得出函数解析式是解决问题关键.

练习册系列答案
相关题目
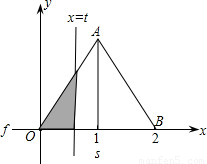
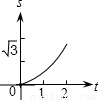
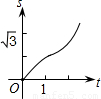
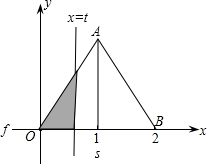 如图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是( )
如图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是( )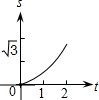
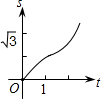
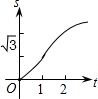
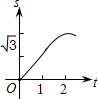
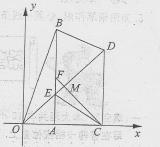
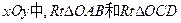 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,