题目内容
 如图,已知C是线段AB的中点,D是线段AC的中点,E是线段BC的中点.
如图,已知C是线段AB的中点,D是线段AC的中点,E是线段BC的中点.(1)若AB=18cm,求DE的长;
(2)若CE=5cm,求DB的长.
分析:(1)先由C是线段AB的中点求出AC和BC,再由D是线段AC的中点,E是线段BC的中点.求出DC和CE,从而求出DE的长;
(2)首先由(1)得出CE和BD的关系,然后求出BD的长.
(2)首先由(1)得出CE和BD的关系,然后求出BD的长.
解答:解:(1)∵C是AB的中点,
∴AC=BC=
AB=9(cm) …(2分)
∵D是AC的中点,
∴AD=DC=
AC=
(cm)
∵E是BC的中点,
∴CE=BE=
BC=
(cm) …(4分)
又∵DE=DC+CE,
∴DE=
+
=9(cm) …(6分)
(2)由(1)知:AD=DC=CE=EB,
∴CE=
BD
∵CE=5cm,
∴BD=15(cm) …(8分)
∴AC=BC=
| 1 |
| 2 |
∵D是AC的中点,
∴AD=DC=
| 1 |
| 2 |
| 9 |
| 2 |
∵E是BC的中点,
∴CE=BE=
| 1 |
| 2 |
| 9 |
| 2 |
又∵DE=DC+CE,
∴DE=
| 9 |
| 2 |
| 9 |
| 2 |
(2)由(1)知:AD=DC=CE=EB,
∴CE=
| 1 |
| 3 |
∵CE=5cm,
∴BD=15(cm) …(8分)
点评:此题考查的知识点是两点间的距离,利用中点性质转化线段之间的倍分关系是解题的关键.

练习册系列答案
相关题目
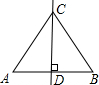 如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )
如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )| A、AE=BE | B、AD=BD | C、AB=AC | D、ED=AD |
如图,已知C是线段AB的中点,则CD等于( )


| A、AD-BD | ||
B、
| ||
C、
| ||
D、AD-
|
 如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE.
如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE. (2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1
(2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1