题目内容
如图，已知B是线段AE上一点，ABCD和BEFG都是正方形，连接AG、CE．（1）求证：AG=CE；
（2）设CE与GF的交点为P，求证：
| PG |
| CG |
| PE |
| AG |
分析：（1）根据正方形的特征，可知AB=CB，BG=BE，∠ABG=∠CBE=90°，根据全等三角形的判定定理，可知△ABG≌△CBE，从而得出AG=CE，
（2）根据正方形的特征，可知PG∥BE，
=
，
=
，再由（1）△ABG≌△CBE，得出BG=BE，AG=CE，从而得出
=
．
（2）根据正方形的特征，可知PG∥BE，
| PG |
| BE |
| CG |
| CB |
| BG |
| CB |
| PE |
| CE |
| PG |
| CG |
| PE |
| AG |
解答：证明：（1）∵四边形ABCD和BEFG是正方形，
∴AB=CB，BG=BE，∠ABG=∠CBE=90°，
∴△ABG≌△CBE，
∴AG=CE，
（2）∵PG∥BE
∴
=
，
=
，
∵BG=BE，AG=CE，
∴
=
，
=
，
∴
=
．
∴AB=CB，BG=BE，∠ABG=∠CBE=90°，
∴△ABG≌△CBE，
∴AG=CE，
（2）∵PG∥BE
∴
| PG |
| BE |
| CG |
| CB |
| BG |
| CB |
| PE |
| CE |
∵BG=BE，AG=CE，
∴
| PG |
| CG |
| BG |
| CB |
| BG |
| CB |
| PE |
| AG |
∴
| PG |
| CG |
| PE |
| AG |
点评：本题主要考查了正方形的性质，全等三角形的判定，全等三角形的性质，比较综合，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
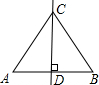如图，已知CD是线段AB的垂直平分线，垂足为D，E是CD上一点．若∠A=60°，则下列结论中错误的是（ ）| A、AE=BE | B、AD=BD | C、AB=AC | D、ED=AD |
如图，已知C是线段AB的中点，则CD等于（ ）
| A、AD-BD | ||
B、
| ||
C、
| ||
D、AD-
|
（2012•宿迁）如图，已知P是线段AB的黄金分割点，且PA＞PB，若S1表示PA为一边的正方形的面积，S2表示长是AB，宽是PB的矩形的面积，则S1