Question

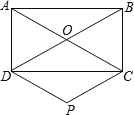
【题目】已知，如图，在矩形ABCD中，对角线AC与BD相交于点O，过点C作BD的平行线，过点D作AC的平行线，两线交于点P．

①求证：四边形CODP是菱形．

②若AD＝6，AC＝10，求四边形CODP的面积．

Answer 1

【答案】①证明见解析；(2)S菱形CODP＝24.

【解析】

① 根据DP∥AC，CP∥BD，即可证出四边形CODP是平行四边形，由矩形的性质得出OC=OD，即可得出结论；

② 利用S△COD＝S菱形CODP，先求出S△COD,即可得.

证明：①∵DP∥AC，CP∥BD

∴四边形CODP是平行四边形，

∵四边形ABCD是矩形，

∴BD＝AC，OD＝BD，OC＝AC，

∴OD＝OC，

∴四边形CODP是菱形．

②∵AD＝6，AC＝10

∴DC＝＝8

∵AO＝CO，

∴S△COD＝S△ADC＝××AD×CD＝12

∵四边形CODP是菱形，

∴S△COD＝S菱形CODP＝12，

∴S菱形CODP＝24