题目内容
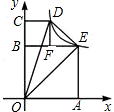 如图,已知四边形AOBE和四边形CBFD均为正方形,反比例函数
如图,已知四边形AOBE和四边形CBFD均为正方形,反比例函数 的图象经过D、E两点,则△DOE的面积等于
的图象经过D、E两点,则△DOE的面积等于
- A.
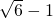
- B.

- C.2
- D.

C
分析:设正方形CBFD的边长为x,根据题意,反比例函数 的图象经过点E,易得E的坐标为(2,2);进而表示出D的坐标,可以得到出AE=OA=2,BC=BF=
的图象经过点E,易得E的坐标为(2,2);进而表示出D的坐标,可以得到出AE=OA=2,BC=BF= -1,EF=3-
-1,EF=3- ;分割图形可得S△DOE=S正方形AOBE+S正方形AOBE+S△DEF-S△OCD-S△OAE,代入数据可得答案.
;分割图形可得S△DOE=S正方形AOBE+S正方形AOBE+S△DEF-S△OCD-S△OAE,代入数据可得答案.
解答:设正方形CBFD的边长为x,
正方形AOBE,且反比例函数 的图象经过点E,易得E的坐标为(2,2);
的图象经过点E,易得E的坐标为(2,2);
故点D的坐标可表示为(x,2+x);
又有反比例函数 的图象经过D,
的图象经过D,
则x•(2+x)=4,解可得x= -1;
-1;
则AE=OA=2,BC=BF= -1,EF=3-
-1,EF=3- ,
,
则S△DOE=S正方形AOBE+S正方形AOBE+S△DEF-S△OCD-S△OAE=2;
故选C.
点评:本题以比例系数k的几何意义为知识基础,结合正方形、三角形的面积计算,涉及面积的分割与计算,难度较大.
分析:设正方形CBFD的边长为x,根据题意,反比例函数
 的图象经过点E,易得E的坐标为(2,2);进而表示出D的坐标,可以得到出AE=OA=2,BC=BF=
的图象经过点E,易得E的坐标为(2,2);进而表示出D的坐标,可以得到出AE=OA=2,BC=BF= -1,EF=3-
-1,EF=3- ;分割图形可得S△DOE=S正方形AOBE+S正方形AOBE+S△DEF-S△OCD-S△OAE,代入数据可得答案.
;分割图形可得S△DOE=S正方形AOBE+S正方形AOBE+S△DEF-S△OCD-S△OAE,代入数据可得答案.解答:设正方形CBFD的边长为x,
正方形AOBE,且反比例函数
 的图象经过点E,易得E的坐标为(2,2);
的图象经过点E,易得E的坐标为(2,2);故点D的坐标可表示为(x,2+x);
又有反比例函数
 的图象经过D,
的图象经过D,则x•(2+x)=4,解可得x=
 -1;
-1;则AE=OA=2,BC=BF=
 -1,EF=3-
-1,EF=3- ,
,则S△DOE=S正方形AOBE+S正方形AOBE+S△DEF-S△OCD-S△OAE=2;
故选C.
点评:本题以比例系数k的几何意义为知识基础,结合正方形、三角形的面积计算,涉及面积的分割与计算,难度较大.

练习册系列答案
相关题目
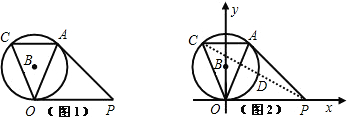
 (2010•北海)如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为
(2010•北海)如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为 如图,已知四边形ABCD中,AD∥BC,AC与BD交于点O,AO=CO,过项点A的直线交BD于点P,交CD于点Q,并交BC的延长线于点R.
如图,已知四边形ABCD中,AD∥BC,AC与BD交于点O,AO=CO,过项点A的直线交BD于点P,交CD于点Q,并交BC的延长线于点R.
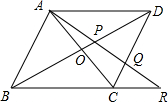 如图,已知四边形ABCD中,AD∥BC,AC与BD交于点O,AO=CO,过项点A的直线交BD于点P,交CD于点Q,并交BC的延长线于点R.
如图,已知四边形ABCD中,AD∥BC,AC与BD交于点O,AO=CO,过项点A的直线交BD于点P,交CD于点Q,并交BC的延长线于点R.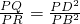 成立吗,若成立,请说明理由.
成立吗,若成立,请说明理由.