Question

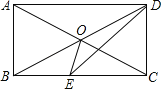
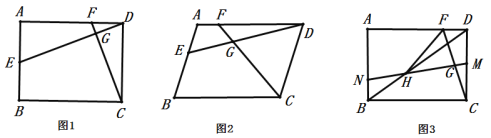
【题目】在平行四边形ABCD中，对角线AC，BD交于点O，E是边AD上的一个动点(与点A，D不重合)，连接EO并延长，交BC于点F，连接BE，DF．下列说法:

① 对于任意的点E，四边形BEDF都是平行四边形;

② 当∠ABC>90°时，至少存在一个点E，使得四边形BEDF是矩形;

③ 当AB<AD时，至少存在一个点E，使得是四边形BEDF是菱形;

④ 当∠ADB=45°时，至少存在一个点E，使得是四边形BEDF是正方形．

所有正确说法的序号是：_________．

Answer 1

【答案】①②③

【解析】

依据平行四边形的性质、平行线的性质、全等三角形的判定及性质得到，依据对角线互相平分的四边形是平行四边形，可得①正确；依据有一个角为直角的平行四边形为矩形，可得②正确；依据大边对大角，可得∠ABD>∠ADB，则至少存在一个点E，使得∠EBD=∠ADB，依据等角对等边得EB=ED，依据临边相等的平行四边形是菱形，可得③正确；当∠ADB=45°时，若∠ABC<45°，则∠ABC<90°，∠EBC<90°，四边形BEDF不可能是正方形，故④错误．

解：①在中，对角线AC，BD相交于点O，

，，,
，，
≌(AAS)，
．
∵，，
四边形AFCE是平行四边形；

② 当∠ABC>90°时，

∴至少存在一个点E，使得∠EBC=90°，

∴BEDF是矩形；

③ 当AB<AD时，∠ABD>∠ADB，

∴至少存在一个点E，使得∠EBD=∠ADB，

∴EB=ED，

∴BEDF是菱形；

④ 当∠ADB=45°时，若∠ABC<45°,

则∠ABC<90°，∠EBC<90°，

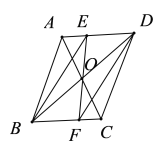
∴四边形BEDF不可能是正方形．

故答案为：①②③.