题目内容
如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD= ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
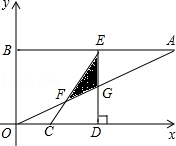
(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t的函数关系式及t的取值范围;
(3)连结DF,
①当t取何值时,有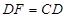 ?
?
②直接写出ΔCDF的外接圆与OA相切时t的值.
 ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t的函数关系式及t的取值范围;
(3)连结DF,
①当t取何值时,有
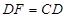 ?
?②直接写出ΔCDF的外接圆与OA相切时t的值.
(1)线段CE的长为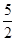 ;
;
(2)S=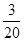 (
(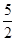 ﹣t)2,t的取值范围为:0≤t≤
﹣t)2,t的取值范围为:0≤t≤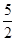 ;
;
(3)①当t=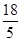 时,DF=CD;②ΔCDF的外接圆与OA相切时t=
时,DF=CD;②ΔCDF的外接圆与OA相切时t=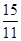 .
.
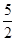 ;
;(2)S=
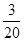 (
(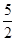 ﹣t)2,t的取值范围为:0≤t≤
﹣t)2,t的取值范围为:0≤t≤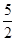 ;
;(3)①当t=
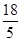 时,DF=CD;②ΔCDF的外接圆与OA相切时t=
时,DF=CD;②ΔCDF的外接圆与OA相切时t=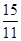 .
.试题分析:(1)直接根据勾股定理求出CE的长即可;
(2)作FH⊥CD于H.,由AB∥OD,DE⊥OD,OB⊥OD可知四边形ODEB是矩形,故可用t表示出AE及BE的长,由相似三角形的判定定理可得出△OCF∽△AEF,△ODG∽△AEG,由相似三角形的性质可用t表示出CF及EG的长,FH∥ED可求出HD的长,由三角形的面积公式可求出S与t的关系式;
(3)①由(2)知CF=t,当DF=CD时,作DK⊥CF于K,则CK=
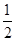 CF=
CF=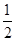 t,CK=CDcos∠DCE,由此可得出t的值;
t,CK=CDcos∠DCE,由此可得出t的值;②先根据勾股定理求出OA的长,由(2)知HD=
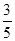 (5﹣t),由相似三角形的判定定理得出Rt△AOB∽Rt△OFH,可用t表示出OF的长,因为当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,由切割线定理可知OF2=OC•OD,故可得出结论.
(5﹣t),由相似三角形的判定定理得出Rt△AOB∽Rt△OFH,可用t表示出OF的长,因为当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,由切割线定理可知OF2=OC•OD,故可得出结论.试题解析:(1)∵在Rt△CDE中,CD=
 ,DE=2,
,DE=2,∴CE=
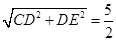 ;
;(2)如图1,作FH⊥CD于H.
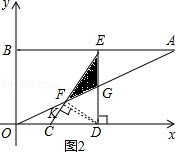
∵AB∥OD,DE⊥OD,OB⊥OD,
∴四边形ODEB是矩形,
∴BE=OD,
∵OC=t,
∴BE=OD=OC+CD=t+
 ,
,∴AE=AB﹣BE=4﹣(t+
 )=
)=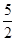 ﹣t,
﹣t,∵AB∥OD,
∴△OCF∽△AEF,△ODG∽△AEG,
∴
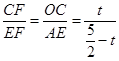 ,
, ,
,又∵CF+EF=5,DG+EG=4,
∴
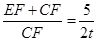 ,
,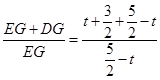 ,
,∴CF=t,EG=
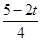 ,
,∴EF=CE﹣CF=5﹣t,
∵FH∥ED,
∴
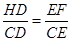 ,即HD=
,即HD= •CD=
•CD=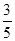 (
(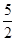 ﹣t),
﹣t),∴S=
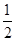 EG•HD=
EG•HD=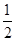 ×
×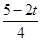 ×
×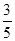 (
(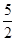 ﹣t)=
﹣t)=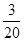 (
(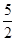 ﹣t)2,
﹣t)2,t的取值范围为:0≤t≤
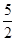 ;
;(3)①由(2)知CF=t,
如图2,当DF=CD时,如图作DK⊥CF于K,
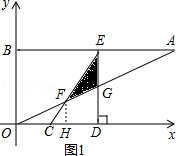
则CK=
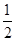 CF=
CF=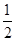 t,
t,∵CK=CDcos∠DCE,
∴
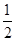 t=3×
t=3×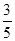 ,
,解得:t=
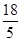 ;
;∴当t=
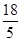 时,DF=CD;
时,DF=CD;②∵点A,B坐标分别为(8,4),(0,4),
∴AB=8,OB=4,
∴OA=
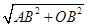 =4
=4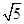 ,
,∵由(2)知HD=
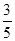 (5﹣t),
(5﹣t),∴OH=t+3﹣
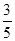 (5﹣t)=
(5﹣t)=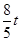 ,
,∵∠A+∠AOB=∠AOD+∠AOB=90°,
∴∠A=∠AOD,
∴Rt△AOB∽Rt△OFH,
∴
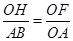 ,
,解得OF=
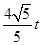 ,
,∵当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,
∴OF2=OC•OD,即(
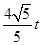 )2=t(t+3),得t=
)2=t(t+3),得t=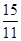 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.
 .
.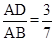 ,则EC的长是( )
,则EC的长是( )
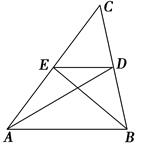
 中,
中, 是
是 的中点,
的中点, 和
和 交于点
交于点 ,设△
,设△ 的面积为
的面积为 ,△
,△ 的面积为
的面积为 ,则下列结论中正确的是( )
,则下列结论中正确的是( )



