题目内容
如图，E是△ABC边BC上的一点，DE垂直平分AB，△ACE的周长是8.5，AB=3，则△ABC的周长为
- A.8.5
- B.10
- C.11.5
- D.13
C
分析：DE垂直平分AB，可得AE=EB，△ABC的周长可以化为△ACE的周长加上AB，根据已知条件可进行求解．
解答：∵DE垂直平分AB，∴AE=EB，
又因为△ACE的周长是8.5，即AC+CE+AE=8.5，
∴△ABC的周长=AC+CE+EB+AB=AC+CE+AE+AB=8.5+3=11.5．
故选C．
点评：本题考查了线段垂直平分线的性质，属于基础题，解题关键是掌握垂直平分线上任意一点到线段两端点的距离相等．
分析：DE垂直平分AB，可得AE=EB，△ABC的周长可以化为△ACE的周长加上AB，根据已知条件可进行求解．
解答：∵DE垂直平分AB，∴AE=EB，
又因为△ACE的周长是8.5，即AC+CE+AE=8.5，
∴△ABC的周长=AC+CE+EB+AB=AC+CE+AE+AB=8.5+3=11.5．
故选C．
点评：本题考查了线段垂直平分线的性质，属于基础题，解题关键是掌握垂直平分线上任意一点到线段两端点的距离相等．
练习册系列答案
相关题目
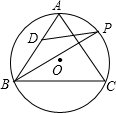如图，D是△ABC边AB上的一点，使得AB=3AD，P是△ABC外接圆上一点（P在弧AC上），使得∠ADP=∠ACB，求
4、如图，D是△ABC边AC上的一点，过D点画线段DE，使点E在△ABC的边上，并且点D，E和△ABC的一个顶点组所在小三角形与△ABC相似，则这样的E点有
如图，P是△ABC边AB上的一点，连接CP，下列条件中，不能判定△ACP∽△ABC的是（ ）| A、AC2=AP•AB | ||||
| B、∠ABC=∠ACP | ||||
| C、∠APC=∠ACB | ||||
D、
|
如图，E是△ABC边BC上的一点，DE垂直平分AB，△ACE的周长是8.5，AB=3，则△ABC的周长为（ ）
已知：如图，D是△ABC边BC上的一点，∠DAC=∠B，