题目内容
如图，P是△ABC边AB上的一点，连接CP，下列条件中，不能判定△ACP∽△ABC的是（ ）| A、AC2=AP•AB | ||||
| B、∠ABC=∠ACP | ||||
| C、∠APC=∠ACB | ||||
D、
|
分析：A、根据两组对应边成比例，且夹角相等的两个三角形相似；
B、C都是根据两个角对应相等，则两个三角形相似；
D、有两组边对应成比例的两个三角形不一定相似．
B、C都是根据两个角对应相等，则两个三角形相似；
D、有两组边对应成比例的两个三角形不一定相似．
解答：解：A、∵AC2=AP•AB，
∴
=
，
又∵∠PAC=∠CAB，
∴△ACP∽△ABC，
故此选项错误；
B、∵∠ABC=∠ACP，
又∵∠PAC=∠CAB，
∴△ACP∽△ABC，
故此选项错误；
C、∵∠APC=∠ABC，
又∵∠PAC=∠CAB，
∴△ACP∽△ABC，
故此选项错误；
D、两组边对应成比例的两个三角形不一定相似，故此选项正确．
故选D．
∴
| AC |
| AP |
| AB |
| AC |
又∵∠PAC=∠CAB，
∴△ACP∽△ABC，
故此选项错误；
B、∵∠ABC=∠ACP，
又∵∠PAC=∠CAB，
∴△ACP∽△ABC，
故此选项错误；
C、∵∠APC=∠ABC，
又∵∠PAC=∠CAB，
∴△ACP∽△ABC，
故此选项错误；
D、两组边对应成比例的两个三角形不一定相似，故此选项正确．
故选D．
点评：本题考查了相似三角形的判定．要对相似三角形的判定定理很熟练．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
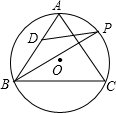如图，D是△ABC边AB上的一点，使得AB=3AD，P是△ABC外接圆上一点（P在弧AC上），使得∠ADP=∠ACB，求
4、如图，D是△ABC边AC上的一点，过D点画线段DE，使点E在△ABC的边上，并且点D，E和△ABC的一个顶点组所在小三角形与△ABC相似，则这样的E点有
如图，E是△ABC边BC上的一点，DE垂直平分AB，△ACE的周长是8.5，AB=3，则△ABC的周长为（ ）
已知：如图，D是△ABC边BC上的一点，∠DAC=∠B，