题目内容
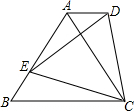 已知:△ABC为等边三角形,AD∥BC,AD=BE.求证:△DEC为等边三角形.
已知:△ABC为等边三角形,AD∥BC,AD=BE.求证:△DEC为等边三角形.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:首先可证明△DAC≌△BEC,由全等三角形的性质可知:CD=CE,所以△DCE为等腰三角形,再通过证明∠DCE=60°即可得到:△DEC为等边三角形.
解答:证明:∵△ABC为等边三角形,
∴AC=BC,∠ABC=∠EBC=60°,
∵AD∥BC,
∴∠DAC=∠ABC,
∴∠DAC=EBC=60°,
在△DAC和△BEC中,
,
∴△DAC≌△BEC(SAS),
∴DC=CE,∠DCA=∠ECB,
∵∠ACB=60°,
∴∠ECD=60°,
∴△DEC为等边三角形.
∴AC=BC,∠ABC=∠EBC=60°,

∵AD∥BC,
∴∠DAC=∠ABC,
∴∠DAC=EBC=60°,
在△DAC和△BEC中,
|
∴△DAC≌△BEC(SAS),
∴DC=CE,∠DCA=∠ECB,
∵∠ACB=60°,
∴∠ECD=60°,
∴△DEC为等边三角形.
点评:本题考查了等边三角形的判定与性质、全等三角形的判定与性质.等边三角形的判定可以通过三个内角相等,三条边都相等或者两条相等的边之间的夹角是60°等方法.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
在有理式
,
(x+y),
,
,
中,分式有( )
| 2 |
| x |
| 1 |
| 3 |
| 5 |
| π-3 |
| x2 |
| a-1 |
| 3x+y |
| 6 |
| A、1个 | B、2个 | C、3个 | D、4个 |
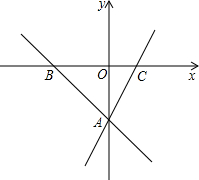 已知一次函数y=mx+m-2与y=2x-3的图象的交点A在y轴上,它们与x轴的交点分别为点B.点C.
已知一次函数y=mx+m-2与y=2x-3的图象的交点A在y轴上,它们与x轴的交点分别为点B.点C. 已知点A与点B (-1,1)关于x轴对称,点C在y轴的负半轴上,且到原点的距离为2,一直线经过点A和点C.
已知点A与点B (-1,1)关于x轴对称,点C在y轴的负半轴上,且到原点的距离为2,一直线经过点A和点C.