题目内容
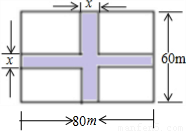
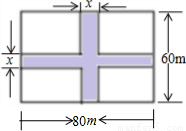
如图，一块草地是长80m、宽60m的矩形，欲在中间修筑两条互相垂直的宽为x m的小路，这时草坪面积为y m2．求y与x的函数关系式，并写出自变量x的取值范围．
解：由题意得：
y=（80-x）（60-x），
=x2-140x+4800（0＜x＜60）．
所以函数关系式为：
y=x2-140x+4800（0＜x＜60）．
分析：可以把两条互相垂直的小路平移到矩形两边上，这样便于表达草坪的长（80-x）m，宽（60-x）m，列出函数关系式．
点评：本题是用矩形面积公式表示函数关系式．
y=（80-x）（60-x），
=x2-140x+4800（0＜x＜60）．
所以函数关系式为：
y=x2-140x+4800（0＜x＜60）．
分析：可以把两条互相垂直的小路平移到矩形两边上，这样便于表达草坪的长（80-x）m，宽（60-x）m，列出函数关系式．
点评：本题是用矩形面积公式表示函数关系式．
练习册系列答案
相关题目
19、如图，一块草地是长80m、宽60m的矩形，欲在中间修筑两条互相垂直的宽为x m的小路，这时草坪面积为y m2．求y与x的函数关系式，并写出自变量x的取值范围．
7、如图，一块草地是长80 m，宽60 m的矩形，欲在中间修筑两条互相垂直的宽为xm的小路，这时草坪面积为y m2．求y与x的函数关系式，并写出自变量x的取值范围是
