题目内容
已知等边△ABC,点D是直线BC上一点,以AD为边在AD的右侧作等边△ADE,连结CE.
(1)如图①,若点D在线段BC上,求证:CE+CD=AB;
(2)如图②,若点D在BC延长线上,线段CD,CE和AB有怎样的数量关系?证明你的结论.
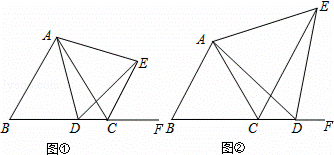
证明:(1)如图①,∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°.
∴∠DAE﹣∠CAD=∠BAC﹣∠CAD.
即∠CAE=∠BAD.
在△CAE和△BAD中,
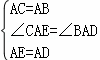 ,
,
∴△CAE≌△BAD(SAS).
∴EC=DB(全等三角形的对应边相等);
∴CE+CD=DB+CD=BC=AB,
即CE+CD=AB;
(2)CE﹣CD=AB;
理由如下:如图②,∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°.
∴∠DAE+∠CAD=∠BAC+∠CAD.
即∠CAE=∠BAD.
在△CAE和△BAD中,
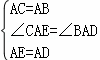 ,
,
∴△CAE≌△BAD(SAS).
∴EC=DB(全等三角形的对应边相等);
∴CE﹣AB=DB﹣BC=CD,即CE﹣CD=AB.


练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目


 的大小,结果正确的是( )
的大小,结果正确的是( ) B.
B.  C.
C.  D.
D. 
 B.
B.  C.
C.  D.
D. 