题目内容
如图的坐标平面上有四直线L1、L2、L3、L4．若这四直线中，有一直线为方程式3x-5y+15=0的图形，则此直线为何？（ ）
A．L1
B．L2
C．L3
D．L4
【答案】分析：求出直线与X、Y轴的交点坐标（0，3），（-5，0），根据图象即可选出答案．
解答：解：将x=0代入3x-5y+15=0得：y=3，
∴方程式3x-5y+15=0的图形与y轴的交点为（0，3），
将y=0代入3x-5y+15=0得：x=-5，
∴方程式3x-5y+15=0的图形与x轴的交点为（-5，0），
观察图形可得直线L1与x、y轴的交点恰为（-5，0）、（0，3），
∴方程式3x-5y+15=0的图形为直线L1．
故选A．
点评：本题主要考查对一次函数的图象，一次函数图象上点的坐标特征等知识点的理解和掌握，能根据一次函数的图象进行判断是接此题的关键．
解答：解：将x=0代入3x-5y+15=0得：y=3，
∴方程式3x-5y+15=0的图形与y轴的交点为（0，3），
将y=0代入3x-5y+15=0得：x=-5，
∴方程式3x-5y+15=0的图形与x轴的交点为（-5，0），
观察图形可得直线L1与x、y轴的交点恰为（-5，0）、（0，3），
∴方程式3x-5y+15=0的图形为直线L1．
故选A．
点评：本题主要考查对一次函数的图象，一次函数图象上点的坐标特征等知识点的理解和掌握，能根据一次函数的图象进行判断是接此题的关键．
练习册系列答案
相关题目
15、如图的坐标平面上有四直线L1、L2、L3、L4．若这四直线中，有一直线为方程式3x-5y+15=0的图形，则此直线为何？（ ）
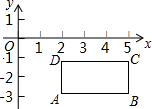如图，平面上有四个点，它们的坐标分别是A（2，-2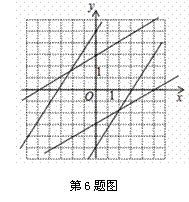
C．3 D．4
如图的坐标平面上有四直线L1、L2、L3、L4．若这四直线中，有一直线为方程式3x-5y+15=0的图形，则此直线为何？