题目内容
5.一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)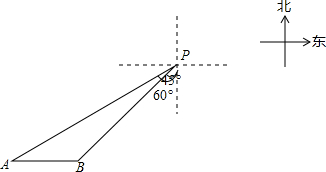
分析 利用题意得到AC⊥PC,∠APC=60°,∠BPC=45°,AB=20海里,如图,设BC=x海里,则AC=AB+BC=(20+x)海里.解△PBC,得出PC=BC=x海里,解Rt△APC,得出AC=PC•tan60°=$\sqrt{3}$x,根据AC不变列出方程$\sqrt{3}$x=20+x,解方程即可.
解答 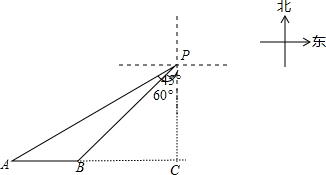 解:如图,AC⊥PC,∠APC=60°,∠BPC=45°,AB=20海里,设BC=x海里,则AC=AB+BC=(20+x)海里.
解:如图,AC⊥PC,∠APC=60°,∠BPC=45°,AB=20海里,设BC=x海里,则AC=AB+BC=(20+x)海里.
在△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,
∴PC=BC=x海里,
在Rt△APC中,∵tan∠APC=$\frac{AC}{PC}$,
∴AC=PC•tan60°=$\sqrt{3}$x,
∴$\sqrt{3}$x=20+x,
解得x=10$\sqrt{3}$+10,
则PC=(10$\sqrt{3}$+10)海里.
答:轮船航行途中与灯塔P的最短距离是(10$\sqrt{3}$+10)海里.
点评 本题考查了解直角三角形的应用-方向角:在辨别方向角问题中:一般是以第一个方向为始边向另一个方向旋转相应度数.在解决有关方向角的问题中,一般要根据题意理清图形中各角的关系,有时所给的方向角并不一定在直角三角形中,需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角.

练习册系列答案
相关题目
20.若x与3互为相反数,则|x+3|等于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.下列二次根式中,最简二次根式是( )
| A. | $-\sqrt{2}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{1}{5}}$ | D. | $\sqrt{a^2}$ |
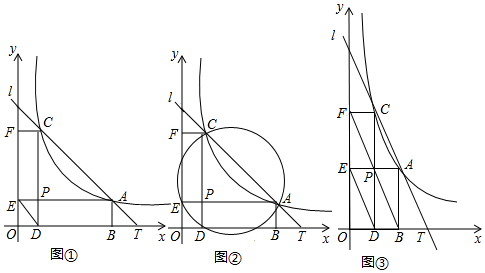
 如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.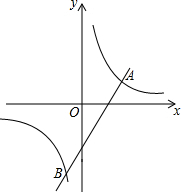 如图,一次函数y=2x-4的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且点A的横坐标为3.
如图,一次函数y=2x-4的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且点A的横坐标为3. 如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为π-2.
如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为π-2.