题目内容
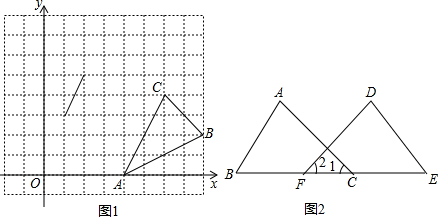
在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:______________;结论:________.(均填写序号)
证明:

【答案】
题设:①②③;结论:④,证明见解析
【解析】解题设:①②③;结论:④.
证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF。
在△ABC和△DEF中,AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS),∴∠1=∠2。
此题可以分成三种情况:
情况一:题设:①②③;结论:④,可以利用SAS定理证明△ABC≌△DEF。
情况二:题设:①③④;结论:②,可以利用AAS证明△ABC≌△DEF:
在△ABC和△DEF中,∵ AB=DE,∠B=∠E,∠1=∠2,∴△ABC≌△DEF(AAS)。
∴BC=EF,∴BC-FC=EF-FC,即BF=EC。
情况三:题设:②③④;结论:①,可以利用ASA证明△ABC≌△DEF,再根据全等三角形的
性质可推出结论:
∵BF=EC,∴BF+CF=EC+CF,即BC=EF。
在△ABC和△DEF中,∵∠B=∠E ,BC=EF,∠1=∠2,∴△ABC≌△DEF(ASA)。∴AB=DE。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 ,并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.
,并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.