Question

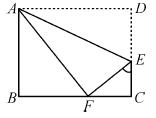
（2013莱芜）如图，在Rt△ABC中，∠ACB＝90°，以AC为一边向外作等边三角形ACD，点E为AB的中点，连接DE．

（1）证明：DE∥CB；

（2）探索AC与AB满足怎样的数量关系时，四边形DCBE是平行四边形．

Answer 1

（1）证明：连接CE．

∵点E为Rt△ACB的斜边AB的中点，

∴

∵△ACD是等边三角形．

∴AD＝CD．

在△ADE与△CDE中，

∴△ADE≌△CDE（SSS），

∴．

∵∠DCB＝90°＋60°＝150°，

∴∠EDC＋∠DCB＝180°．

∴DE∥CB．

（2）【解析】
∵∠DCB＝150°，若四边形DCBE是平行四边形，则DC∥BE，∠DCB＋∠B＝180°．∠B＝30°．

在Rt△ACB中，有．

∴当时，四边形DCBE是平行四边形．

【解析】此题主要考查了平行线的判定、全等三角形的判定与性质，以及平行四边形的判定，关键是掌握直角三角形的性质，以及等边三角形的性质．