题目内容
14.(1)若9m•27m-1÷33m=27,求m的值;(2)若10m=20,10n=$\frac{1}{5}$,求9m÷32n.
分析 (1)根据幂的乘方,可化成同底数幂的运算,根据同底数幂的乘除法,可得关于m的方程,根据解方程,可得答案;
(2)由10m=20,10n=$\frac{1}{5}$,利用同底数幂的除法的性质,即可求得m-n的值,又由9m÷32n=32(m-n),即可求得答案.
解答 解;(1)由幂的乘方,得
32m•33m-3×33m=33.
由同底数幂的乘除法,得
32m+(3m-3)+3m=33.
2m+3m+3+3m=3.
解得m=0;
(2)∵10m=20,10n=$\frac{1}{5}$,
∴10m-n=10m÷10n=100=102,
∴m-n=2,
∴9m÷32n=32m÷32n=32m-2n=32(m-n)=34=81.
点评 本题考查了同底数幂的除法,利用了幂的乘方,同底数幂的乘除法.

练习册系列答案
相关题目
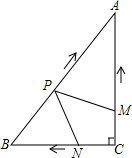 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点M,N从但C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN设移动时间为t(单位:秒,0<t<2.5)
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点M,N从但C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN设移动时间为t(单位:秒,0<t<2.5)