题目内容
 如图:已知等腰三角形ABC中,AB=AC,D是BC边上的一点,DE⊥AB,DF⊥AC,E,F分别为垂足.DE+DF=2
如图:已知等腰三角形ABC中,AB=AC,D是BC边上的一点,DE⊥AB,DF⊥AC,E,F分别为垂足.DE+DF=2| 2 |
| 2 |
| 6 |
分析:连接AD,然后根据S△ABC=S△ABD+S△ACD列出方程,求解即可.
解答: 解:如图,连接AD,S△ABC=S△ABD+S△ACD,
解:如图,连接AD,S△ABC=S△ABD+S△ACD,
=
AB•DE+
AC•DF,
=
AB(DE+DF),
∵DE+DF=2
,
∴
AB×2
=(3
+2
),
∴AB=
=3+2
.
 解:如图,连接AD,S△ABC=S△ABD+S△ACD,
解:如图,连接AD,S△ABC=S△ABD+S△ACD,=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
∵DE+DF=2
| 2 |
∴
| 1 |
| 2 |
| 2 |
| 2 |
| 6 |
∴AB=
3
| ||||
|
| 3 |
点评:本题考查了二次根式的应用,主要利用了二次根式的除法运算,作辅助线把△ABC分成两个三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
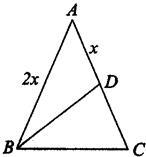 22、如图,已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分,求它的底边BC的长.
22、如图,已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分,求它的底边BC的长. 如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB.
如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB.
 15、如图,已知等腰三角形ABC中,AC=BC,D为BC边上一点,且AB=AD,若不再添加辅助线,图中与∠C相等的角是
15、如图,已知等腰三角形ABC中,AC=BC,D为BC边上一点,且AB=AD,若不再添加辅助线,图中与∠C相等的角是 如图,已知等腰三角形ABC,顶点A的坐标是(
如图,已知等腰三角形ABC,顶点A的坐标是(