题目内容
 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=30°,然后朝着旗杆方向前进到点D,测得∠ADB=45°,量得CD=20
如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=30°,然后朝着旗杆方向前进到点D,测得∠ADB=45°,量得CD=20 -20,求旗杆AB的高.
-20,求旗杆AB的高.
解:设AB=x,
∵∠ACB=30°,
∴BC=AB•cot30°= x,
x,
∵∠ADB=45°,
∴BD=AB•cot45°=x,
∴CD=BC-BD=( -1)x=20
-1)x=20 -20,
-20,
解得x=20.
故旗杆AB的高度为20.
分析:设AB=x,则根据∠ACB=30°和∠ADB=45°可以求得BC、BD的长度(用x表示),根据CD=BC-BD即可求得x的值,即AB的高.
点评:本题考查了特殊角的三角函数值,直角三角形中各边的关系,本题中正确计算三角函数值是解题的关键.
∵∠ACB=30°,
∴BC=AB•cot30°=
 x,
x,∵∠ADB=45°,
∴BD=AB•cot45°=x,
∴CD=BC-BD=(
 -1)x=20
-1)x=20 -20,
-20,解得x=20.
故旗杆AB的高度为20.
分析:设AB=x,则根据∠ACB=30°和∠ADB=45°可以求得BC、BD的长度(用x表示),根据CD=BC-BD即可求得x的值,即AB的高.
点评:本题考查了特殊角的三角函数值,直角三角形中各边的关系,本题中正确计算三角函数值是解题的关键.

练习册系列答案
相关题目
 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=30°,然后朝着旗杆方向前进到点D,测得∠ADB=45°,量得CD=20
如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=30°,然后朝着旗杆方向前进到点D,测得∠ADB=45°,量得CD=20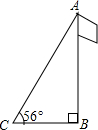 (2012•广西)如图,为测量旗杆AB的高度,在与B距离为8米的C处测得旗杆顶端A的仰角为56°,那么旗杆的高度约是
(2012•广西)如图,为测量旗杆AB的高度,在与B距离为8米的C处测得旗杆顶端A的仰角为56°,那么旗杆的高度约是 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高.
如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高. 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高.
如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高.