题目内容
 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高.
如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高.
解:∵∠ACB=15°,∠ADB=30°,
∴∠CAD=∠ADB-∠ACB=30°-15°=15°,
即△CAD为等腰三角形,
∴AD=CD=13,
在△ADB中,∵AB⊥DB,∠ADB=30°,
∴AB= AD=
AD= ×13=6.5m.
×13=6.5m.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CAD,再根据等角对等边的性质可得AD=CD,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等角对等边的性质,熟记性质是解题的关键.
∴∠CAD=∠ADB-∠ACB=30°-15°=15°,
即△CAD为等腰三角形,
∴AD=CD=13,
在△ADB中,∵AB⊥DB,∠ADB=30°,
∴AB=
 AD=
AD= ×13=6.5m.
×13=6.5m.分析:根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CAD,再根据等角对等边的性质可得AD=CD,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等角对等边的性质,熟记性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=30°,然后朝着旗杆方向前进到点D,测得∠ADB=45°,量得CD=20
如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=30°,然后朝着旗杆方向前进到点D,测得∠ADB=45°,量得CD=20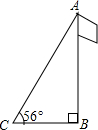 (2012•广西)如图,为测量旗杆AB的高度,在与B距离为8米的C处测得旗杆顶端A的仰角为56°,那么旗杆的高度约是
(2012•广西)如图,为测量旗杆AB的高度,在与B距离为8米的C处测得旗杆顶端A的仰角为56°,那么旗杆的高度约是 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高.
如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高. 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=30°,然后朝着旗杆方向前进到点D,测得∠ADB=45°,量得CD=20
如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=30°,然后朝着旗杆方向前进到点D,测得∠ADB=45°,量得CD=20 -20,求旗杆AB的高.
-20,求旗杆AB的高.