��Ŀ����
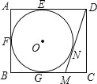
����Ŀ����1�� ��ͼ1��ʾ��BD��CD�ֱ��ǡ�ABC���ڽǡ�ABC����ACB��ƽ���ߣ���˵������D=90��+![]() ��A��
��A��

��2��̽������ֱ��д��������������Ľ��������ѡһ�����˵�����ɣ�
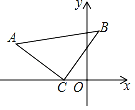
����ͼ2��ʾ��BD��CD�ֱ��ǡ�ABC������ǡ�EBC�͡�FCB��ƽ���ߣ���̽����A���D֮��ĵ�����ϵ��
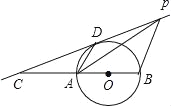
����ͼ3��ʾ��BD��CD�ֱ��ǡ�ABCһ���ڽǡ�ABC��һ����ǡ�ACE��ƽ���ߣ���̽����A���D֮��ĵ�����ϵ��
���𰸡���1��֤������������2���١�A=180��2��D�����ɼ��������ڡ�A=2��D�����ɼ�����
��������
��1���������ý�ƽ�������ʵó���DBC=![]() ��ABC����DCB=
��ABC����DCB=![]() ��ACB���������������ڽǺͶ����ó���A+��ABC+��ACB=180���Լ���DBC+��DCB+��D=180�����ݴ˽�һ�����Ա�����֤���ɣ�
��ACB���������������ڽǺͶ����ó���A+��ABC+��ACB=180���Լ���DBC+��DCB+��D=180�����ݴ˽�һ�����Ա�����֤���ɣ�
��2�����������ɽ�ƽ�������ʵó���EBC=2��DBC����FCB=2��DCB��Ȼ���������������ڽǺ����ʽ�һ�������ó���A2(��DBC+��DCB)=-180�����ݴ˽�һ�����Է���֤�����ɣ�������������������ʿ�֪��DCE=��DBC+��D��Ȼ�������ý�ƽ�������ʵó�2��DBC=��ABC��2��DCE=��ACE������ٽ�ϡ�A+��ABC=��ACE��һ��֤������.
��1����BD��CD�ֱ��ǡ�ABC����ACB��ƽ���ߣ�
���DBC=![]() ��ABC����DCB=
��ABC����DCB=![]() ��ACB��
��ACB��
�ߡ�A+��ABC+��ACB=180����
���ABC+��ACB=180����A��
�֡ߡ�DBC+��DCB+��D=180����
���D=180��(��DBC+��DCB)
=180��![]() (��ABC+��ACB)
(��ABC+��ACB)
=180��![]() (180����A)
(180����A)
=180��90��+![]() ��A
��A
=90��+![]() ��A��
��A��
������D=90��+![]() ��A��
��A��
��2���١�A=180��2��D���������£�
��BD��CD�ֱ��ǡ�EBC�͡�FCB��ƽ���ߣ�
���EBC=2��DBC����FCB=2��DCB��
�ߡ�A+��ABC+��ACB=180����
���ABC=180��(��A+��ACB)=180��2��DBC��
��ACB=180��(��A+��ABC)=180��2��DCB��
���A+180��2��DBC+180��2��DCB=180����
���A2(��DBC+��DCB)=180����
�֡ߡ�DBC+��DCB+��D=180����
���DBC+��DCB=180����D��
���A2(��DBC+��DCB)=��A2(180����D)=180����
������A360��+2��D=180����
��2��D=180����A��
������A=180��2��D��
�ڡ�A=2��D���������£�
�ߡ�DCE�ǡ�ABC��һ����ǣ�
���DCE=��DBC+��D��
��BD��CD�ֱ��ǡ�ABC�͡�ACE��ƽ���ߣ�
��2��DBC=��ABC��2��DCE=��ACE��
�ߡ�A+��ABC=��ACE��
���A+2��DBC=2��DCE��
���A+2��DBC=2��DBC+2��D��
���A=2��D.