题目内容
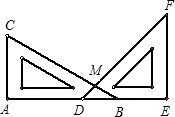如图，将三角尺ABC和三角尺DEF（其中∠A=∠E=90°，∠C=60°，∠F=45°）摆放在一起，使得点A、D、B、E在同一条直线上，BC交DF于点M，那么∠CMF角度等于
- A.120°
- B.105°
- C.90°
- D.75°
B
分析：利用直角三角形的两个锐角互余求得∠ABC与∠FDE的度数，然后在△MDB中，利用三角形内角和定理求得∠DMB，再依据对顶角相等即可求解．
解答：∵直角△ABC中，∠ABC=90°-∠C=90°-60°=30°，
同理，∠FDE=90°-∠F=90°-45°=45°，
∴∠DMB=180°-∠ABC-∠FDE=180°-30°-45°=105°，
∴∠CMF=∠DMB=105°．
故选B．
点评：本题考查了三角形的内角和定理，以及对顶角的性质，正确求得∠DMB的度数是关键．
分析：利用直角三角形的两个锐角互余求得∠ABC与∠FDE的度数，然后在△MDB中，利用三角形内角和定理求得∠DMB，再依据对顶角相等即可求解．
解答：∵直角△ABC中，∠ABC=90°-∠C=90°-60°=30°，
同理，∠FDE=90°-∠F=90°-45°=45°，
∴∠DMB=180°-∠ABC-∠FDE=180°-30°-45°=105°，
∴∠CMF=∠DMB=105°．
故选B．
点评：本题考查了三角形的内角和定理，以及对顶角的性质，正确求得∠DMB的度数是关键．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
9、如图，将三角尺ABC（其中∠ABC=60°，∠C=90°）绕B点按顺时针方向转动一个角度到A1BC1的位置，使得点A，B，C1在同一条直线上，那么这个角度等于（ ）
如图，将三角尺ABC（其中∠ABC=60°，∠C=90°）绕点B按顺时针转动一个角度到A1BC1的位置，使得点A、B、C1在同一条直线上，那么这个角度等于
如图，将三角尺ABC（其中∠B=60°，∠C=90°，AB=6）绕点B按顺时针转动一个角度到A1BC1的位置，使得点A、B、C1在同一条直线上，点A所经过的路程是（ ）
如图，将三角尺ABC（其中∠A=30°，∠C=90°）绕B点按顺时针方向转动一个角度到△A′BC′的位置，使得点A、B、C′在同一条直线上，则这个角度等于（ ）
（1）如图，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如果AF=4，AB=7：