Question

解下列不等式（组），并把解集在数轴上表示出来
（1）

x+1

6

＜

2x-5

4

+1                        
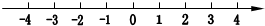
（2）

1 2 (3-x)≤3 1-x 2 ≥ x-1 3

Answer 1

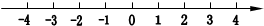
分析：（1）根据不等式的性质，先去分母，然后去括号，之后移项合并同类相即可；
（2）根据不等式的性质分别求出①②的解集，再求出二者的公共部分即为不等式组的解集，再在数轴上表示出来．

解答：（1）解：原不等式可化为：2（x+1）＜3（2x-5）+12，（2分）
去括号得，2x+2＜6x-15+12，
移项合并同类项得，-4x＜-5，（3分）
x＞

5

4

，（4分）
数轴表示为：
（5分）

（2）解不等式①，得x≥-3，（2分）
解不等式②，得x≤

4

5

，（4分）
不等式组的解为：-3≤x≤

4

5

，（5分）
数轴表示为：

点评：此题主要考查了此题考查了不等式组的解集，求不等式的公共解，要遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．