题目内容
如图,已知OA⊥OB,OA=4,OB=3,以AB为边作矩形ABCD,使AD=![]() ,过点D作DE垂直OA的延长线,且交于点E.
,过点D作DE垂直OA的延长线,且交于点E.
(1)证明:△OAB∽△EDA;
(2)当![]() 为何值时,△OAB与△EDA全等?请说明理由;并求出此时B、D两点的距离.
为何值时,△OAB与△EDA全等?请说明理由;并求出此时B、D两点的距离.

(1)证明:如图示,
∵OA⊥OB ,∴∠1与∠2互余 ……………1分
又∵四边形ABCD是矩形,∴∠BAD=90o,
∴∠2与∠3互余,∴∠1=∠3, ……………2分
∵OA⊥OB,DE⊥OA,∴∠BOA=∠DEA=90o ……………3分
∴△OAB∽△EDA. ……………4分
(2) 解:在Rt△OAB中,AB=![]() ,……………5分
,……………5分
由(1)可知∠1=∠3,∠BOA=∠DEA=90o,
∴当![]() =AD=AB=5时,△OAB与△EDA全等. ……………6分
=AD=AB=5时,△OAB与△EDA全等. ……………6分
当![]() =AD=AB=5时,可知矩形ABCD为正方形 ……………7分
=AD=AB=5时,可知矩形ABCD为正方形 ……………7分
所以此时 BD=![]() ……………8分
……………8分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 17、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有( )
17、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有( ) 长线交于点E.
长线交于点E. 如图,已知OA=OB,那么数轴上点A与点C的距离是
如图,已知OA=OB,那么数轴上点A与点C的距离是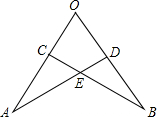 如图,已知OA=OB,OC=OD,下列结论中(1)∠A=∠B;(2)DE=CE;(3)连OE,OE平分∠O,正确的有
如图,已知OA=OB,OC=OD,下列结论中(1)∠A=∠B;(2)DE=CE;(3)连OE,OE平分∠O,正确的有