题目内容
如图，点D，E分别为AB、AC上的两点且DE与BC不平行，请你添加任意一个条件，使△ABC与△ADE相似，添加的条件为∠ADE=∠C或∠AED=∠B或
=
| AE |
| AB |
| AD |
| AC |
∠ADE=∠C或∠AED=∠B或
=
（填一个即可）．| AE |
| AB |
| AD |
| AC |
分析：根据相似三角形判定定理：两个角相等的三角形相似；夹角相等，对应边成比例的两个三角形相似，即可解题．
解答：解：∵∠ADE是公共角，
如∠ADE=∠C或∠AED=∠B，
∴△ADE∽△ABC；
如
=
，
∴△ADE∽△ABC．
故答案为：∠ADE=∠C或∠AED=∠B或
=
．
如∠ADE=∠C或∠AED=∠B，
∴△ADE∽△ABC；
如
| AE |
| AB |
| AD |
| AC |
∴△ADE∽△ABC．
故答案为：∠ADE=∠C或∠AED=∠B或
| AE |
| AB |
| AD |
| AC |
点评：此题主要考查学生对相似三角形判定的理解和掌握，此题答案不唯一，具有较强的开放性．
练习册系列答案
相关题目
如图，点D、E分别为ABC边AC、AB上的一点，BD、CE交于点O，且BO=3DO，CO=3EO．求证：DE∥BC．
如图，点D、E分别为△ABC的边AB、AC的中点，已知BC=6cm，则DE=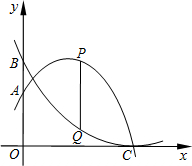
0）．点P、Q分别在抛物线y=
如图，点C、E分别为△ABD的边BD、AB上两点，且AE=AD，CE=CD，∠D=70゜，