题目内容
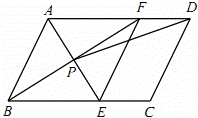
正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.

(1)依题意补全图1;
(2)若∠PAB=20°,求∠ADF的度数;
(3)如图2,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.
解:(1)如图1所示:
(2)如图2,连接AE,
则∠PAB=∠PAE=20°,AE=AB=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAP=∠BAP=20°,
∴∠EAD=130°,
∴∠ADF= =25°;
=25°;
(3)如图3,连接AE、BF、BD,
由轴对称的性质可得:EF=BF,AE=AB=AD,
∠ABF=∠AEF=∠ADF,
∴∠BFD=∠BAD=90°,
∴BF2+FD2=BD2,
∴EF2+FD2=2AB2.



 名校名卷单元同步训练测试题系列答案
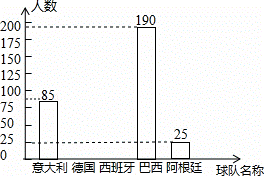
名校名卷单元同步训练测试题系列答案2014年世界杯足球赛于北京时间6月 13日 2时在巴西开 幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意 大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最 有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被 调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一 队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:
| 球队名称 | 百分比 |
| 意大利 | 17% |
| 德国 | a |
| 西班牙 | 10% |
| 巴西 | 38% |
| 阿根廷 | 0 |
根据统计图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)根据以上信息,请直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.
不等式组 的解集是( )
的解集是( )
|
| A. |
| B. | ﹣ | C. | ﹣ | D. | ﹣ |
下列四个图形中,既是轴对称图形又是中心对称图形的是( )
|
| A. |
| B. |
| C. |
| D. |
|
 <x≤2
<x≤2



 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论: