题目内容
设a，b，c满足abc≠0，a+b=c，则
+
的值为（ ）
| b2+c2-a2 |
| 2bc |
| a2+b2-c2 |
| 2ab |
| A、0 | B、1 | C、2 | D、-2 |
分析：把已知的式子变形得到a-c=-b，c-b=a，然后把所求式子第一项的分子一三项结合，利用平方差公式分解因式后，把a+b=c代入，然后分子分母约分后，再变形，把a-c=-b代入即可求出值；第二项的分子一三项结合，利用平方差公式分解因式，把a-c=-b代入，约分后再变形，把c-b=a代入即可求出值，求出两式之和即可得到原式的值．
解答：解：∵a+b=c，
∴a-c=-b，c-b=a，
则
+
=
+
=
+
=
+
=
+
=
+
=
+
=1+（-1）=0．
故选A．
∴a-c=-b，c-b=a，
则
| b2+c2-a2 |
| 2bc |
| a2+b2-c2 |
| 2ab |
=
| b2-a2+c2 |
| 2bc |
| a2-c2+b2 |
| 2ab |
=
| (b+a)(b-a)+c2 |
| 2bc |
| (a+c)(a-c)+b2 |
| 2ab |
=
| c(b-a)+c2 |
| 2bc |
| -b(a+c)+b2 |
| 2ab |
=
| b-a+c |
| 2b |
| -a-c+b |
| 2a |
=
| b-(a-c) |
| 2b |
| -a-(c-b) |
| 2a |
=
| b-(-b) |
| 2b |
| -a-a |
| 2a |
=1+（-1）=0．
故选A．
点评：此题考查了分式的化简求值，要求学生熟练掌握平方差公式，多次利用整体代换的思想来求解，熟练掌握平方差公式及整体代入的思想是解本题的关键．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
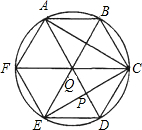如图，圆内接六边形ABCDEF满足AB=CD=EF，且对角线AD、BE、CF相交于一点Q，设AD与CF的交点为P．
