题目内容
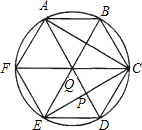
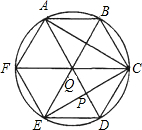如图，圆内接六边形ABCDEF满足AB=CD=EF，且对角线AD、BE、CF相交于一点Q，设AD与CF的交点为P．求证：（1）
| QD |
| ED |
| AC |
| EC |
| CP |
| PE |
| AC2 |
| CE2 |
分析：（1）由AB=CD=EF，根据考查了在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等得到弧AB=弧CD=弧EF，得∠AEB=∠CED，得到∠QED=∠BEC+∠CED=∠BEC+∠AEB=∠AEC，则△QDE∽△ACE，即有
=
；
（2）由弧CD=弧EF，得到DE∥CF，则
=
，∠CQD=∠QDE，而∠QED对BD弧，∠ADC对AC弧，所以∠QED=∠ADC，证得△QCD∽△DEQ，于是有
=
，即QC=
，得到
=
=
，再利用（1）的结论即可得到
=
．
| QD |
| ED |
| AC |
| EC |
（2）由弧CD=弧EF，得到DE∥CF，则
| CP |
| PE |
| QC |
| DE |
| QC |
| DQ |
| DQ |
| DE |
| DQ2 |
| DE |
| CP |
| PE |
| QC |
| DE |
| DQ2 |
| DE2 |
| CP |
| PE |
| AC2 |
| CE2 |
解答：
证明：（1）连AE，
∵AB=CD=EF，
∴弧AB=弧CD=弧EF，
∴∠AEB=∠CED，
∴∠QED=∠BEC+∠CED=∠BEC+∠AEB=∠AEC，
又∵∠QDE=∠ACE，
∴△QDE∽△ACE，
∴
=
；
（2）∵弧CD=弧EF，
∴DE∥CF，
∴
=
，∠CQD=∠QDE，
∵∠QED对BD弧，∠ADC对AC弧，
而DC弧=AB弧，
∴∠QED=∠ADC，
∴△QDC∽△DEQ，
∴
=
，即QC=
，
∴
=
=
，
由（1）的结论
=
得，
=
=
=
．
证明：（1）连AE，∵AB=CD=EF，
∴弧AB=弧CD=弧EF，
∴∠AEB=∠CED，
∴∠QED=∠BEC+∠CED=∠BEC+∠AEB=∠AEC，
又∵∠QDE=∠ACE，
∴△QDE∽△ACE，
∴
| QD |
| ED |
| AC |
| EC |
（2）∵弧CD=弧EF，
∴DE∥CF，
∴
| CP |
| PE |
| QC |
| DE |
∵∠QED对BD弧，∠ADC对AC弧，
而DC弧=AB弧，
∴∠QED=∠ADC，
∴△QDC∽△DEQ，
∴
| QC |
| DQ |
| DQ |
| DE |
| DQ2 |
| DE |
∴
| CP |
| PE |
| QC |
| DE |
| DQ2 |
| DE2 |
由（1）的结论
| QD |
| ED |
| AC |
| EC |
| CP |
| PE |
| QC |
| DE |
| DQ2 |
| DE2 |
| AC 2 |
| EC2 |
点评：本题考查了在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等．也考查了三角形相似的判定与性质．
练习册系列答案
相关题目
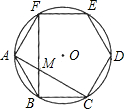如图，圆内接正六边形ABCDEF中，AC、BF交于点M．则S△ABM：S△AFM=
（1997•陕西）如图，圆内接正六边形ABCDEF中，AC，BF相交于点O，则S△ABO：S△AFO=
如图，圆内接六边形ABCDEF满足AB=CD=EF，且对角线AD、BE、CF相交于一点Q，设AD与CF的交点为P．
；（2）
．