题目内容
21、已知，如图，等边△ABC中，D为AC的中点，CE为BC的延长线，且CE=CD．求证：BD=DE．
分析：根据等边三角形的性质得到∠DBC=30°，∠ACB=60°，再根据角之间的关系可得到∠DBC=∠E=30°，即BD=DE．
解答：证明：∵等边△ABC中，D为AC的中点，
∴∠DBC=30°，∠ACB=60°．
∵DC=CE，
∴∠E=∠CDE．
∵∠ACB=∠E+∠EDC=60°，
∴∠E=∠CDE=30°．
∴∠DBC=∠E=30°．
∴BD=DE．
∴∠DBC=30°，∠ACB=60°．
∵DC=CE，
∴∠E=∠CDE．
∵∠ACB=∠E+∠EDC=60°，
∴∠E=∠CDE=30°．
∴∠DBC=∠E=30°．
∴BD=DE．
点评：此题主要考查学生对等边三角形的性质的理解及运用；进行角的等量代换是正确解答本题的关键．
练习册系列答案
相关题目
明理由；
已知：如图，等边△ABC的边长为6，点D、E分别在AB、AC上，且AD=AE=2，直线l过点A，且l∥BC，若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动，设F点运动的时间为t秒，当t＞0时，直线DF交l于点G，GE的延长线与BC的延长线交于点H，AB与GH相交于点O．
已知，如图，等边三角形ABC边长为2，以BC为对称轴将△ABC翻折，得到四边形ABDC，将此四边形放在直角坐标系xOy中，使AB在x轴上，点D在直线
已知：如图，等边△ABC的边长为2，E为BC边的中点，分别以顶点B、C为圆心，BE、CE长为半径画弧交AB、AC于点D、F．求图中阴影部分的面积．
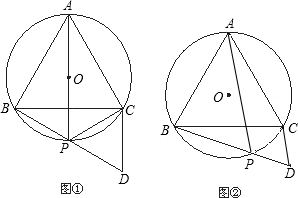
已知：如图，等边三角形ABD与等边三角形ACE具有公共顶点A，连接CD，BE，交于点P．