题目内容
已知：如图，等边△ABC的边长为2，E为BC边的中点，分别以顶点B、C为圆心，BE、CE长为半径画弧交AB、AC于点D、F．求图中阴影部分的面积．
分析：根据题意先求得AE，再求出S扇形BED=S扇形CEF，以及S△ABC．从而得出S阴影ADEF=S△ABC-2S扇形BED．
解答：
解：∵△ABC是等边三角形，
∴∠B=∠C=60°．
∵E为BC边的中点，BC=2，
∴BE=CE=1．且AE⊥BC．
∴AE=
=
．
∴S扇形BED=S扇形CEF=
=
π．
∴S△ABC=
×2×
=
．
∴S阴影ADEF=S△ABC-2S扇形BED=
-
π．
解：∵△ABC是等边三角形，∴∠B=∠C=60°．
∵E为BC边的中点，BC=2，
∴BE=CE=1．且AE⊥BC．
∴AE=
| AB2-BE2 |
| 3 |
∴S扇形BED=S扇形CEF=
| 60×π×12 |
| 360 |
| 1 |
| 6 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
∴S阴影ADEF=S△ABC-2S扇形BED=
| 3 |
| 1 |
| 3 |
点评：本题考查了扇形面积的计算，能得出阴影部分的面积等于S阴影ADEF=S△ABC-2S扇形BED，是解此题的关键．
练习册系列答案
相关题目
明理由；
已知：如图，等边△ABC的边长为6，点D、E分别在AB、AC上，且AD=AE=2，直线l过点A，且l∥BC，若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动，设F点运动的时间为t秒，当t＞0时，直线DF交l于点G，GE的延长线与BC的延长线交于点H，AB与GH相交于点O．
已知，如图，等边三角形ABC边长为2，以BC为对称轴将△ABC翻折，得到四边形ABDC，将此四边形放在直角坐标系xOy中，使AB在x轴上，点D在直线
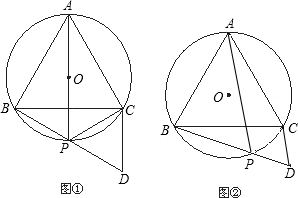
已知：如图，等边三角形ABD与等边三角形ACE具有公共顶点A，连接CD，BE，交于点P．