题目内容
8.先化简,再求值:$(1-\frac{1}{a-1})÷\frac{{{a^2}-4a+4}}{{{a^2}-a}}$,其中-2<a≤2,请选择一个a的合适整数代入求值.分析 根据分式的减法和除法可以化简题目中的式子,然后在-2<a≤2中,选择一个使得原分式的值有意义的a的整数值代入即可解答本题.
解答 解:$(1-\frac{1}{a-1})÷\frac{{{a^2}-4a+4}}{{{a^2}-a}}$
=$\frac{a-1-1}{a-1}•\frac{a(a-1)}{(a-2)^{2}}$
=$\frac{a-2}{a-1}•\frac{a(a-1)}{(a-2)^{2}}$
=$\frac{a}{a-2}$,
当a=-1时,原式=$\frac{-1}{-1-2}=\frac{1}{3}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法,注意最后代入的a的值首先要使得原分式有意义,还要是整数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.如图,①是一个三角形,分别连接这个三角形三边中点得到图②,再连接图②中间小三角形三边的中点得到图③,按这样的方法进行下去,第⑨个图形中共有三角形的总数为( )
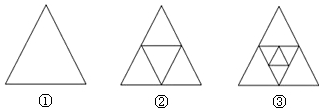

| A. | 33个 | B. | 36个 | C. | 37个 | D. | 41个 |
13.下列8个数中:$-\root{3}{8}$,0.131131113…(相邻两个3之间依次多一个1),0,sin45°,$\sqrt{25}$,-π,$\frac{22}{7}$,$-\sqrt{27}$,无理数的个数有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
17.下列计算正确的是( )
| A. | 20170=0 | B. | $\sqrt{81}$=±9 | C. | (x2)3=x5 | D. | 3-1=$\frac{1}{3}$ |
18.内角为108°的正多边形是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
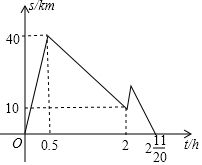 甲、乙两辆汽车同时从A地出发前往相距250千米的B地,乙车先出发匀速行驶,一段时间后,甲车出发匀速追赶,途中因油料不足,甲到服务区加油花了6分钟,为了尽快追上乙车,甲车提高速度仍保持匀速行驶,追上乙车后继续保持这一速度直到B地,如图是甲、乙两车之间的距离s(km2),乙车出发时间t(h)之间的函数关系图象,则甲车比乙车早到11.5分钟.
甲、乙两辆汽车同时从A地出发前往相距250千米的B地,乙车先出发匀速行驶,一段时间后,甲车出发匀速追赶,途中因油料不足,甲到服务区加油花了6分钟,为了尽快追上乙车,甲车提高速度仍保持匀速行驶,追上乙车后继续保持这一速度直到B地,如图是甲、乙两车之间的距离s(km2),乙车出发时间t(h)之间的函数关系图象,则甲车比乙车早到11.5分钟. 如图所示的几何体是由四个完全相同的正方体组成的,这个几何体的俯视图是( )
如图所示的几何体是由四个完全相同的正方体组成的,这个几何体的俯视图是( )


