题目内容
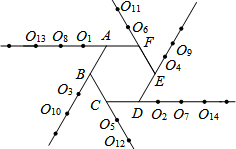将正六边形ABCDEF的各边按如图所示延长，从射线FA开始，分别在各射线上标记点O1，O2，O3，…，按此规律，则点O2013所在射线是
- A.AB
- B.DE
- C.BC
- D.EF
B
分析：把射线FA，AB，CD，BC，DE，EF上面的点分别列举，再找到规律，由规律即可求出点A2013所在的射线．
解答：从射线FA开始，分别在各射线上标记点O1，O2，O3，…，按此规律，得出：
FA→CD→AB→DE→BC→EF→CD→FA→DE→AB→EF→BC→FA→CD→AB…
故点O1，O2，O3，…，每12次一循环，
∵2013÷12=167…9，
∴点O2013所在射线与第9次标记相同，
故点O2013所在射线是DE．
故选：B．
点评：本题考查了点的坐标规律，是一个规律探索题，可以列出点的排列规律从中得到规律，在变化的点中找到其排列直线的不变的规律，此类问题的排列通常是具有周期性，按照周期循环，难度适中．
分析：把射线FA，AB，CD，BC，DE，EF上面的点分别列举，再找到规律，由规律即可求出点A2013所在的射线．
解答：从射线FA开始，分别在各射线上标记点O1，O2，O3，…，按此规律，得出：
FA→CD→AB→DE→BC→EF→CD→FA→DE→AB→EF→BC→FA→CD→AB…
故点O1，O2，O3，…，每12次一循环，
∵2013÷12=167…9，
∴点O2013所在射线与第9次标记相同，
故点O2013所在射线是DE．
故选：B．
点评：本题考查了点的坐标规律，是一个规律探索题，可以列出点的排列规律从中得到规律，在变化的点中找到其排列直线的不变的规律，此类问题的排列通常是具有周期性，按照周期循环，难度适中．
练习册系列答案
相关题目
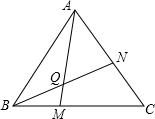
（1）如图，正△ABC中，点M与点N分别是BC、CA上的点，且BM=CN，连接AM、BN，两线交于点Q，求∠AQN的度数．
（2）将1题中的“正△ABC”分别改为正方形ABCD，正五边形ABCDE，正六边形ABCDEF，…，正n边形ABCD…N，其余条件不变，根据第1题的求解思路分别推断∠AQN的度数，将结论填入下表：
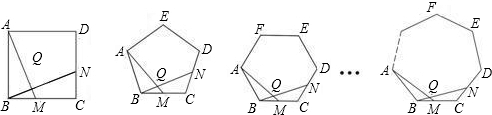
（2）将1题中的“正△ABC”分别改为正方形ABCD，正五边形ABCDE，正六边形ABCDEF，…，正n边形ABCD…N，其余条件不变，根据第1题的求解思路分别推断∠AQN的度数，将结论填入下表：
| 正多边形 | 正方形 | 正五边形 | 正六边形 | … | 正n边形 |
| ∠AQN的度数 |
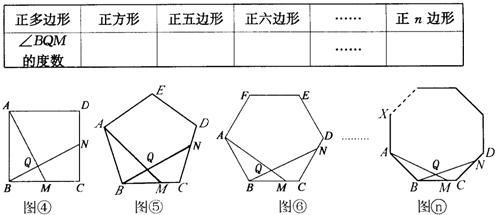
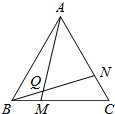（1）已知△ABC为正三角形，点M是BC上一点，点N是AC上一点，AM、BN相交于点Q，∠BAM=∠NBC，猜想∠BQM等于多少度，并证明你的猜想．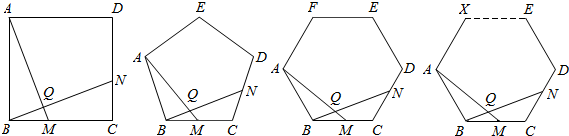
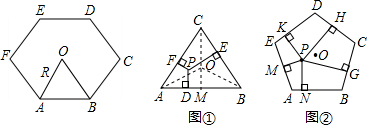（2012•青岛模拟）同学们已经认识了很多正多边形，现以正六边形为例再介绍与正多边形相关的几个概念．如正六边形ABCDEF各边对称轴的交点O，又称正六边形的中心，其中OA称正六边形的半径，通常用R表示，∠AOB称为中心角，显然．提出问题：正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系？
