Question

【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AF、BE是△ABC的中线，AF⊥BE于点P，像△ABC这样的三角形称为“中垂三角形”．设BC=a，AC=b，AB=c．

（特例探究）

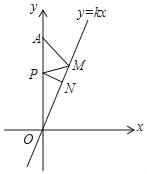
（1）如图1，当tan∠PAB=1，c=2时，a=　 　，b=　 　；

如图2，当∠PAB=30°，c=4时，a=　 　，b=　 　；

（归纳证明）

（2）请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．

（拓展证明）

（3）如图4，ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=6，AB=6，求AF的长．

Answer 1

【答案】（1）4，4，，；（2）猜想：a 2，b2，c2三者之间的关系是：a2+b2=5c2（3）AF=2

【解析】

试题(1)①由等腰直角三角形的性质得到AP=BP=AB=4，根据三角形中位线的性质,得到EF∥AB，EF=AB=2，再由勾股定理得到结果；②如图2，连接EF，类比①，结合△PEF～△ABP进行求解；

(2)连接EF，类比着(1)即可证得结论;

(3)根据全等三角形的性质得到AG=GF，得到BG是△ABF的中线,取AB的中点H,连接FH,并延长交DA的延长线于P,推出四边形CSPF是平行四边形,根据平行四边形的性质得到FP∥CE,得到△ABF是中垂三角形,于是得到结论.

解：（1）∵AF⊥BE，∠ABE=45°，

∴AP=BP=AB=4，

∵AF，BE是△ABC的中线，

∴EF∥AB，EF=AB=2，

∴∠PFE=∠PEF=45°，

∴PE=PF=2，

在Rt△FPB和Rt△PEA中，

AE=BF==2，

∴AC=BC=4，

∴a=b=4，

如图2，连接EF，

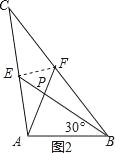
同理可得：EF=×2=1，

∵EF∥AB，

∴△PEF～△ABP，

∴=，

在Rt△ABP中，

AB=2，∠ABP=30°，

∴AP=1，PB=，

∴PF=，PE=，

在Rt△APE和Rt△BPF中，

AE=，BF=，

∴a=，b=，

故答案为：4，4，，；

（2）猜想：a 2，b2，c2三者之间的关系是：a2+b2=5c2，

证明：如图3，连接EF，

∵AF，BE是△ABC的中线，

∴EF是△ABC的中位线，

∴EF∥AB．且 EF=AB=c．

∴==，

设 PF=m，PE=n 则AP=2m，PB=2n，

在Rt△APB中，（2m）2+（2n）2=c2①

在Rt△APE中，（2m）2+n2=（）2②

在Rt△BPF中，m2+（2n）2=（）2③

由①得：m2+n2=，由②+③得：5（ m2+n2）=，

∴a 2+b2=5 c2；

（3）在△AGE与△FGB中，

，

∴△AGE≌△FGB，

∴BG=EG，AG=GF，

∴BG是△ABF的中线，

如图4，取AB的中点H，连接FH，并延长交DA的延长线于P，

同理，△APH≌△BFH，

∴AP=BF，PE=CF=2BF，

∴PE∥CF，PE=CF，

∴四边形CSPF是平行四边形，

∴FP∥CE，

∵BE⊥CE，

∴FP⊥BE，即FH⊥BG，

∴△ABF是中垂三角形，

由（2）知，AB2+AF2=5BF2，

∵AB=6，BF=AD=2，

∴36+AF2=5×（2）2，

∴AF=2．