题目内容
如图.反比例函数y=- 与一次函数y=-x+2的图象交于A、B两点.
与一次函数y=-x+2的图象交于A、B两点.(1)求A、B两点的坐标;
(2)求△AOB的面积.

【答案】分析:(1)解由两个函数组成的方程组;
(2)S△AOB=S△AOD+S△BOD,求出D点坐标后易求其面积.
解答:解:(1)解方程组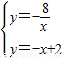 ,
,
得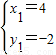 和
和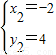 .
.
∴A、B两点的坐标分别为A(-2,4)、B(4,-2).
(2)∵直线y=-x+2与y轴交点D的坐标是(0,2),
∴S△AOD= ×2×2=2,S△BOD=
×2×2=2,S△BOD= ×2×4=4,
×2×4=4,
∴S△AOB=2+4=6.
点评:(1)求交点坐标就是解由函数组成的方程组.(2)本题利用了图形的分割转化思想.
(2)S△AOB=S△AOD+S△BOD,求出D点坐标后易求其面积.
解答:解:(1)解方程组
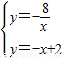 ,
,得
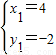 和
和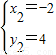 .
.∴A、B两点的坐标分别为A(-2,4)、B(4,-2).
(2)∵直线y=-x+2与y轴交点D的坐标是(0,2),
∴S△AOD=
 ×2×2=2,S△BOD=
×2×2=2,S△BOD= ×2×4=4,
×2×4=4,∴S△AOB=2+4=6.
点评:(1)求交点坐标就是解由函数组成的方程组.(2)本题利用了图形的分割转化思想.

练习册系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数