题目内容
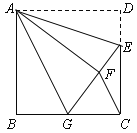
【题目】(1)如图1,在△ABC中,BD是△ABC的角平分线,点D在AC上,DE∥BC,交AB于点E,∠A=50°,∠ADB=110°,求△BDE各内角的度数;


(2)完成下列推理过程.
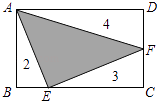
已知:如图2,AD⊥BC,EF⊥BC,∠1=∠2,求证:DG∥AB.推理过程:因为AD⊥BC,EF⊥BC(已知),
所以∠EFB=∠ADB=90°(________).
所以EF∥AD(同位角相等,两直线平行).
所以∠1=∠BAD(________).
因为∠1=∠2(已知),
所以________=________(等量代换).
所以DG∥AB(内错角相等,两直线平行).
【答案】(1)∠ABD=![]() ,
,![]() =20,
=20,![]() =140;(2)垂直的定义;两直线平行,同位角相等;
=140;(2)垂直的定义;两直线平行,同位角相等;![]() ,
,![]()
【解析】
(1)由∠BDC-∠A求出∠ABD的度数,由BD为角平分线得到∠DBC的度数,再由DE与BC平行,利用两直线平行内错角相等求出∠BDE的度数,利用三角形的内角和定理即可求出∠BED的度数;
(2)由AD垂直于BC,EF垂直于BC,利用垂直的定义得到一对直角相等,利用同位角相等两直线平行得到EF与AD平行,利用两直线平行同位角相等得到一对角相等,再由已知一对角相等,利用等量代换得到一对内错角相等,利用内错角相等两直线平行即可得证.
(1)因为![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() 是
是![]() 的角平分线,
的角平分线,
所以![]() .
.
因为![]() ,
,
所以![]() (两直线平行,内错角相等),
(两直线平行,内错角相等),
所以![]() (三角形内角和定理);
(三角形内角和定理);
(2)因为AD⊥BC,EF⊥BC(已知),
所以∠EFB=∠ADB=90°(垂直的定义).
所以EF∥AD(同位角相等,两直线平行).
所以∠1=∠BAD(两直线平行,同位角相等).
因为∠1=∠2(已知),
所以![]() =
=![]() (等量代换).
(等量代换).
所以DG∥AB(内错角相等,两直线平行).
故答案为:垂直的定义;两直线平行,同位角相等;![]() ,
,![]() .
.