题目内容
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
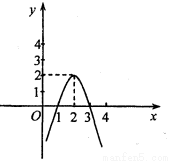
(1)写出y>0时,x的取值范围 ;
(2)写出y随x的增大而减小的自变量x的取值范围 ;
(3)求函数y=ax2+bx+c的表达式.
(1) 1<x<3;(2) x>2;(3) y=-2x2+8x-6.
【解析】
试题分析:(1)y>0是抛物线在x轴上方的部分,而抛物线与x轴交于(1,0),(3,0),结合图象,直接写出x的取值范围;
(2)抛物线的增减性是以对称轴分界的,根据对称轴及开口方向可确定此时自变量x的取值范围;
(3)可以通过已知抛物线与x轴的交点,设交点式;也可以设顶点式.
试题解析:(1)抛物线开口向下,与x轴交于(1,0),(3,0),
当y>0时,x的取值范围是:1<x<3;
(2)抛物线对称轴为直线x=2,开口向下,
y随x的增大而减小的自变量x的取值范围是x>2;
(3)抛物线与x轴交于(1,0),(3,0),
设解析式y=a(x-1)(x-3),把顶点(2,2)代入,
得2=a(2-1)(2-3),解得a=-2,
∴y=-2(x-1)(x-3),
即y=-2x2+8x-6.
考点:1.待定系数法求二次函数解析式;2.二次函数的图象.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(本题满分8分)某公司欲招聘业务员一名,现对A、B、C三名候选人分别进行笔试、面试测试,成绩如下表:
测试项目 | 测试成绩(分) | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 85 | 90 |
面试 | 93 | 75 | 72 |
(1)如果按照三人测试成绩的平均成绩录取人选,那么谁将被录用?
(2)根据实际需要,公司想将丙录用,请兼顾笔试、面试两个方面,你确定的方案是什么?写出理由.
 、
、 为两个连续的整数,且
为两个连续的整数,且 <
< <
< ,则
,则 = .
= . +kx+b经过点P(2,-3),Q(-1,0).
+kx+b经过点P(2,-3),Q(-1,0).
 ,与
,与 轴交点为
轴交点为 .求
.求 的值.
的值. 轴的另一个交点为
轴的另一个交点为 ,求四边形
,求四边形 的面积.
的面积.
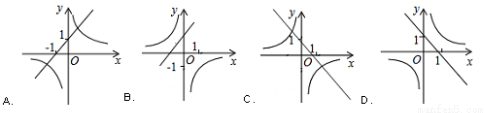
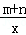 的图象可能是( )
的图象可能是( )
 ,AB=10,则AC的长为
,AB=10,则AC的长为 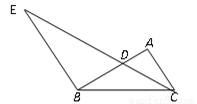
 的两根为
的两根为 、
、 ,则
,则 的值为( )
的值为( ) D.
D.