题目内容
下列结论错误的是
- A.三个角度之比为1：2：3的三角形是直角三角形
- B.三个边长之比为3：4：5的三角形是直角三角形
- C.三个边长之比为8：16：17的三角形是直角三角形
- D.三个角度之比为1：1：2的三角形是直角三角形
C
分析：根据勾股定理的逆定理及三角形的内角和公式进行分析，从而得到答案．
解答：A、因为根据三角形内角和定理可求出三个角分别为30°，60°，90°，所以该结论正确；
B、因为其三边符合勾股定理的逆定理，所以该结论正确；
C、因为其三边不符合勾股定理的逆定理，所以该结论不正确；
D、因为根据三角形内角和定理可求出三个角分别为45°，45°，90°，所以该结论正确．
故选C．
点评：本题考查了直角三角形的判定：可用勾股定理的逆定理判定和求出一角等于90°来判定．
分析：根据勾股定理的逆定理及三角形的内角和公式进行分析，从而得到答案．
解答：A、因为根据三角形内角和定理可求出三个角分别为30°，60°，90°，所以该结论正确；
B、因为其三边符合勾股定理的逆定理，所以该结论正确；
C、因为其三边不符合勾股定理的逆定理，所以该结论不正确；
D、因为根据三角形内角和定理可求出三个角分别为45°，45°，90°，所以该结论正确．
故选C．
点评：本题考查了直角三角形的判定：可用勾股定理的逆定理判定和求出一角等于90°来判定．
练习册系列答案
相关题目
5、如图，已知△ACF≌△BDE，且点E与点F，点A与点B是对应点，下列结论错误的是（ ）
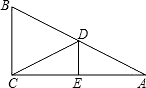如图，△ABC中，∠ACB=90°，DE是AC的中垂线，则下列结论错误的是（ ）A、BC=
| ||
B、CD=
| ||
C、DE=
| ||
| D、AB2=AC2+BC2 |
如图，OB是∠AOC的平分线，OD是∠COE的平分线，如果∠AOB=50°，∠COE=60°，则下列结论错误的是（ ）| A、∠AOE=110° | B、∠BOD=80° | C、∠BOC=50° | D、∠DOE=30° |
（2013•威海）如图，在△ABC中，∠A=36°，AB=AC，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD，下列结论错误的是（ ）