题目内容
已知x的取值能使|x-3|+|x+2|取得最小值,则所有
中整数有( )
| x |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:由题意已知x的取值能使|x-3|+|x+2|取得最小值,可以分类讨论①x≥3;②-2≤<3;③x<-2,求出x的范围,然后把x代入
中,进行求解.
| x |
| 2 |
解答:解:∵已知x的取值能使|x-3|+|x+2|取得最小值,
∴当x≥3时,有|x-3|+|x+2|=x-3+x+2=2x-1,∴当x=3时有最小值:2×3-1=5;
∴当-2<x<3时,有|x-3|+|x+2|=3-x+x+2=5,∴其有最小值5;
当x≤-2时,有|x-3|+|x+2|=3-x-x-2=1-2x,∴当x=-2时有最小值5,
∴-2≤x≤3可以使|x-3|+|x+2|取得最小值,
∴-1≤
≤
,
∴所有
中整数有-1,0,1,共3个,
故选C.
∴当x≥3时,有|x-3|+|x+2|=x-3+x+2=2x-1,∴当x=3时有最小值:2×3-1=5;
∴当-2<x<3时,有|x-3|+|x+2|=3-x+x+2=5,∴其有最小值5;
当x≤-2时,有|x-3|+|x+2|=3-x-x-2=1-2x,∴当x=-2时有最小值5,
∴-2≤x≤3可以使|x-3|+|x+2|取得最小值,
∴-1≤
| x |
| 2 |
| 3 |
| 2 |
∴所有
| x |
| 2 |
故选C.
点评:此题主要考查绝对值的性质和分类讨论的思想,解题时思路要清晰,此题是一道基础题.

练习册系列答案
相关题目
我市高新技术开发区的某公司,用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工.已知生产这种产品每件还需成本费40元.经过市场调查发现:该产品的销售单价,需定在200元到300元之间较为合理,销售单价x元与年销售量y万件之间的变化可近似的看作是如下表所反映的一次函数:
(1)请求出y与x间的函数关系式;并直接写出自变量x的取值范围;
(2)请说明投资的第一年,该公司是盈利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损多少?
(3)在(2)的前提下,即在第一年盈利最大或亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利达1790万元,若能,求出第二年的产品售价;若不能,请说明理由.
| 销售单价x(元) | 200 | 230 | 250 |
| 年销售量y(万件) | 10 | 7 | 5 |
(2)请说明投资的第一年,该公司是盈利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损多少?
(3)在(2)的前提下,即在第一年盈利最大或亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利达1790万元,若能,求出第二年的产品售价;若不能,请说明理由.
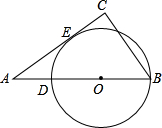 且与BC所在直线相交?
且与BC所在直线相交?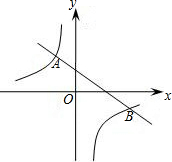 如图,已知一次函数
如图,已知一次函数 中整数有
中整数有