题目内容
已知E是正方形ABCD的一边AB上任一点，AC与BD是正方形ABCD的对角线EG⊥BD于G，EF⊥AC于F，AC=10厘米，则EF+EG=________．
5cm
分析：在AB上任做一点E，做EF垂直AC于F，EG垂直BD于G．连接AC与BD交于O．根据ABCD是正方形，求得△AEF，△BEG是等腰直角三角形．即可解题．
解答：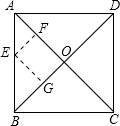
解：在AB上任作一点E，做EF垂直AC于F，EG垂直BD于G．连接AC与BD交于O．
∵ABCD是正方形，AC，BD是对角线，
∴∠ABD，∠BAC=45度．
∴△AEF，△BEG是等腰直角三角形．
∴AF=EF．
∵AC⊥BD，
∴EFOG是矩形．
∴EG=FO．
∴EF+EG=AF+FO=AO=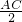
=5cm
点评：此题主要考查学生对正方形的性质的理解和掌握，同时应用了等腰三角形的性质．关键是在AB上任做一点E，做EF垂直AC于F，EG垂直BD于G，连接AC与BD交于O，这是此题的突破点．
分析：在AB上任做一点E，做EF垂直AC于F，EG垂直BD于G．连接AC与BD交于O．根据ABCD是正方形，求得△AEF，△BEG是等腰直角三角形．即可解题．
解答：
解：在AB上任作一点E，做EF垂直AC于F，EG垂直BD于G．连接AC与BD交于O．∵ABCD是正方形，AC，BD是对角线，
∴∠ABD，∠BAC=45度．
∴△AEF，△BEG是等腰直角三角形．
∴AF=EF．
∵AC⊥BD，
∴EFOG是矩形．
∴EG=FO．
∴EF+EG=AF+FO=AO=
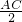=5cm点评：此题主要考查学生对正方形的性质的理解和掌握，同时应用了等腰三角形的性质．关键是在AB上任做一点E，做EF垂直AC于F，EG垂直BD于G，连接AC与BD交于O，这是此题的突破点．
练习册系列答案
相关题目
