题目内容
如图,直线y=kx+b(b>0)与抛物线 相交于点A(x1,y1),B(x2,y2)两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且kS+32=0.
相交于点A(x1,y1),B(x2,y2)两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且kS+32=0.(1)求b的值;
(2)求证:点(y1,y2)在反比例函数
 的图象上;
的图象上;(3)求证:x1•OB+y2•OA=0.

【答案】分析:(1)先求出直线y=kx+b与x轴正半轴交点D的坐标及与y轴交点C的坐标,得到△OCD的面积S=- ,再根据kS+32=0,及b>0即可求出b的值;
,再根据kS+32=0,及b>0即可求出b的值;
(2)先由y=kx+8,得x= ,再将x=
,再将x= 代入y=
代入y= x2,整理得y2-(16+8k2)y+64=0,然后由已知条件直线y=kx+8与抛物线
x2,整理得y2-(16+8k2)y+64=0,然后由已知条件直线y=kx+8与抛物线 相交于点A(x1,y1),B(x2,y2)两点,知y1,y2是方程y2-(16+8k2)y+64=0的两个根,根据一元二次方程根与系数的关系得到y1•y2=64,即点(y1,y2)在反比例函数
相交于点A(x1,y1),B(x2,y2)两点,知y1,y2是方程y2-(16+8k2)y+64=0的两个根,根据一元二次方程根与系数的关系得到y1•y2=64,即点(y1,y2)在反比例函数 的图象上;
的图象上;
(3)先由勾股定理,得出OA2= +
+ ,OB2=
,OB2= +
+ ,AB2=(x1-x2)2+(y1-y2)2,由(2)得y1•y2=64,又易得x1•x2=-64,则OA2+OB2=AB2,根据勾股定理的逆定理得出∠AOB=90°.再过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,根据两角对应相等的两三角形相似证明△AEO∽△OFB,由相似三角形对应边成比例得到
,AB2=(x1-x2)2+(y1-y2)2,由(2)得y1•y2=64,又易得x1•x2=-64,则OA2+OB2=AB2,根据勾股定理的逆定理得出∠AOB=90°.再过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,根据两角对应相等的两三角形相似证明△AEO∽△OFB,由相似三角形对应边成比例得到 =
= ,即可证明x1•OB+y2•OA=0.
,即可证明x1•OB+y2•OA=0.
解答:(1)解:∵直线y=kx+b(b>0)与x轴正半轴相交于点D,与y轴相交于点C,
∴令x=0,得y=b;令y=0,x=- ,
,
∴△OCD的面积S= (-
(- )•b=-
)•b=- .
.
∵kS+32=0,
∴k(- )+32=0,
)+32=0,
解得b=±8,
∵b>0,
∴b=8;
(2)证明:由(1)知,直线的解析式为y=kx+8,即x= ,
,
将x= 代入y=
代入y= x2,得y=
x2,得y= (
( )2,
)2,
整理,得y2-(16+8k2)y+64=0.
∵直线y=kx+8与抛物线 相交于点A(x1,y1),B(x2,y2)两点,
相交于点A(x1,y1),B(x2,y2)两点,
∴y1,y2是方程y2-(16+8k2)y+64=0的两个根,
∴y1•y2=64,
∴点(y1,y2)在反比例函数 的图象上;
的图象上;
(3)证明:由勾股定理,得
OA2= +
+ ,OB2=
,OB2= +
+ ,AB2=(x1-x2)2+(y1-y2)2,
,AB2=(x1-x2)2+(y1-y2)2,
由(2)得y1•y2=64,
同理,将y=kx+8代入y= x2,
x2,
得kx+8= x2,即x2-8kx-64=0,
x2,即x2-8kx-64=0,
∴x1•x2=-64,
∴AB2= +
+ +
+ +
+ -2x1•x2-2y1•y2=
-2x1•x2-2y1•y2= +
+ +
+ +
+ ,
,
又∵OA2+OB2= +
+ +
+ +
+ ,
,
 ∴OA2+OB2=AB2,
∴OA2+OB2=AB2,
∴△OAB是直角三角形,∠AOB=90°.
如图,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F.
∵∠AOB=90°,
∴∠AOE=90°-∠BOF=∠OBF,
又∵∠AEO=∠OFB=90°,
∴△AEO∽△OFB,
∴ =
= ,
,
∵OE=-x1,BF=y2,
∴ =
= ,
,
∴x1•OB+y2•OA=0.
点评:本题是二次函数的综合题型,其中涉及到的知识点有二次函数、反比例函数图象上点的坐标特征,三角形的面积,一次函数与二次函数的交点,一元二次方程根与系数的关系,勾股定理及其逆定理,相似三角形的判定与性质,综合性较强,难度适中.求出△OCD的面积S是解第(1)问的关键;根据函数与方程的关系,得到y1,y2是方程y2-(16+8k2)y+64=0的两个根,进而得出y1•y2=64是解第(2)问的关键;根据函数与方程的关系,一元二次方程根与系数的关系,勾股定理及其逆定理得出∠AOB=90°,是解第(3)问的关键.
 ,再根据kS+32=0,及b>0即可求出b的值;
,再根据kS+32=0,及b>0即可求出b的值;(2)先由y=kx+8,得x=
 ,再将x=
,再将x= 代入y=
代入y= x2,整理得y2-(16+8k2)y+64=0,然后由已知条件直线y=kx+8与抛物线
x2,整理得y2-(16+8k2)y+64=0,然后由已知条件直线y=kx+8与抛物线 相交于点A(x1,y1),B(x2,y2)两点,知y1,y2是方程y2-(16+8k2)y+64=0的两个根,根据一元二次方程根与系数的关系得到y1•y2=64,即点(y1,y2)在反比例函数
相交于点A(x1,y1),B(x2,y2)两点,知y1,y2是方程y2-(16+8k2)y+64=0的两个根,根据一元二次方程根与系数的关系得到y1•y2=64,即点(y1,y2)在反比例函数 的图象上;
的图象上;(3)先由勾股定理,得出OA2=
 +
+ ,OB2=
,OB2= +
+ ,AB2=(x1-x2)2+(y1-y2)2,由(2)得y1•y2=64,又易得x1•x2=-64,则OA2+OB2=AB2,根据勾股定理的逆定理得出∠AOB=90°.再过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,根据两角对应相等的两三角形相似证明△AEO∽△OFB,由相似三角形对应边成比例得到
,AB2=(x1-x2)2+(y1-y2)2,由(2)得y1•y2=64,又易得x1•x2=-64,则OA2+OB2=AB2,根据勾股定理的逆定理得出∠AOB=90°.再过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,根据两角对应相等的两三角形相似证明△AEO∽△OFB,由相似三角形对应边成比例得到 =
= ,即可证明x1•OB+y2•OA=0.
,即可证明x1•OB+y2•OA=0.解答:(1)解:∵直线y=kx+b(b>0)与x轴正半轴相交于点D,与y轴相交于点C,
∴令x=0,得y=b;令y=0,x=-
 ,
,∴△OCD的面积S=
 (-
(- )•b=-
)•b=- .
.∵kS+32=0,
∴k(-
 )+32=0,
)+32=0,解得b=±8,
∵b>0,
∴b=8;
(2)证明:由(1)知,直线的解析式为y=kx+8,即x=
 ,
,将x=
 代入y=
代入y= x2,得y=
x2,得y= (
( )2,
)2,整理,得y2-(16+8k2)y+64=0.
∵直线y=kx+8与抛物线
 相交于点A(x1,y1),B(x2,y2)两点,
相交于点A(x1,y1),B(x2,y2)两点,∴y1,y2是方程y2-(16+8k2)y+64=0的两个根,
∴y1•y2=64,
∴点(y1,y2)在反比例函数
 的图象上;
的图象上;(3)证明:由勾股定理,得
OA2=
 +
+ ,OB2=
,OB2= +
+ ,AB2=(x1-x2)2+(y1-y2)2,
,AB2=(x1-x2)2+(y1-y2)2,由(2)得y1•y2=64,
同理,将y=kx+8代入y=
 x2,
x2,得kx+8=
 x2,即x2-8kx-64=0,
x2,即x2-8kx-64=0,∴x1•x2=-64,
∴AB2=
 +
+ +
+ +
+ -2x1•x2-2y1•y2=
-2x1•x2-2y1•y2= +
+ +
+ +
+ ,
,又∵OA2+OB2=
 +
+ +
+ +
+ ,
, ∴OA2+OB2=AB2,
∴OA2+OB2=AB2,∴△OAB是直角三角形,∠AOB=90°.
如图,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F.
∵∠AOB=90°,
∴∠AOE=90°-∠BOF=∠OBF,
又∵∠AEO=∠OFB=90°,
∴△AEO∽△OFB,
∴
 =
= ,
,∵OE=-x1,BF=y2,
∴
 =
= ,
,∴x1•OB+y2•OA=0.
点评:本题是二次函数的综合题型,其中涉及到的知识点有二次函数、反比例函数图象上点的坐标特征,三角形的面积,一次函数与二次函数的交点,一元二次方程根与系数的关系,勾股定理及其逆定理,相似三角形的判定与性质,综合性较强,难度适中.求出△OCD的面积S是解第(1)问的关键;根据函数与方程的关系,得到y1,y2是方程y2-(16+8k2)y+64=0的两个根,进而得出y1•y2=64是解第(2)问的关键;根据函数与方程的关系,一元二次方程根与系数的关系,勾股定理及其逆定理得出∠AOB=90°,是解第(3)问的关键.

练习册系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
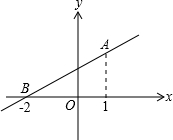 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为