题目内容
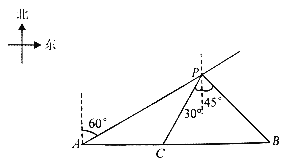
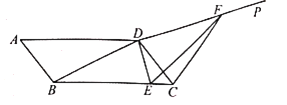
【题目】如图,在![]() 中,
中,![]() ,对角线
,对角线![]() ,点E是线段BC上的动点,连接DE,过点D作DP⊥DE,在射线DP上取点F,使得
,点E是线段BC上的动点,连接DE,过点D作DP⊥DE,在射线DP上取点F,使得![]() ,连接CF,则
,连接CF,则![]() 周长的最小值为___________.
周长的最小值为___________.
【答案】![]()
【解析】
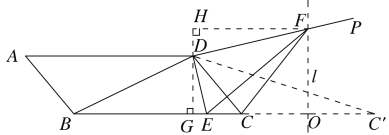
过D作DG⊥BC于点G,过F作FH⊥DG于点H,利用tan∠DBC=![]() 和BD=10可求出DG和BG的长,然后求出CD的长,可知△DCF周长最小,即CF+DF最小,利用“一线三垂直”得到△HDF∽△GED,然后根据对应边成比例推出FH=2GD,可知F在DG右侧距离2DG的直线
和BD=10可求出DG和BG的长,然后求出CD的长,可知△DCF周长最小,即CF+DF最小,利用“一线三垂直”得到△HDF∽△GED,然后根据对应边成比例推出FH=2GD,可知F在DG右侧距离2DG的直线![]() 上,作C点关于直线
上,作C点关于直线![]() 的对称点C',连接DC',DC'的长即为CF+DF的最小值,利用勾股定理求出DC',则CD+DC'的长即为周长最小值.
的对称点C',连接DC',DC'的长即为CF+DF的最小值,利用勾股定理求出DC',则CD+DC'的长即为周长最小值.
如图,过D作DG⊥BC于点G,过F作FH⊥DG于点H,
∵tan∠DBC=![]() ,BD=10,设DG=x,BG=2x
,BD=10,设DG=x,BG=2x
∴![]() ,解得
,解得![]()
∴DG=![]() ,BG=
,BG=![]()
∴GC=BC-BG=![]()
∴CD=![]()
△DCF周长最小,即CF+DF最小
∵∠FDE=90°
∴∠HDF+∠GDE=90°
∵∠GED+∠GDE=90°
∴∠HDF=∠GED
又∵∠DHF=∠EGD=90°
∴△HDF∽△GED
∴![]()
∴FH=2GD=![]()
即F在DG右侧距离![]() 的直线
的直线![]() 上运动,如图所示,
上运动,如图所示,
作C点关于直线![]() 的对称点C',连接DC',DC'的长即为CF+DF的最小值
的对称点C',连接DC',DC'的长即为CF+DF的最小值
∵DG⊥BC,FH⊥DG,FO⊥CC'
∴四边形HFOG为矩形,
∴OG=HF=![]()
又∵GC=![]()
∴OC=OC'=![]()
∴GC'=![]()
在Rt△DGC'中,DC'=![]()
∴△DCF周长的最小值=CD+DC'=![]()
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目