题目内容
 如图,某条河的两岸建有两座楼房.已知写字楼AB的高为80米,小明站在河对岸的一座办公楼CD的楼顶C点处,测得写字楼的楼顶A点处的仰角为60°,测得楼底B点处的俯角为30°.求两座楼房的底部BD之间的距离.
如图,某条河的两岸建有两座楼房.已知写字楼AB的高为80米,小明站在河对岸的一座办公楼CD的楼顶C点处,测得写字楼的楼顶A点处的仰角为60°,测得楼底B点处的俯角为30°.求两座楼房的底部BD之间的距离.
(参考数据: ,计算结果保留3个有效数字)
,计算结果保留3个有效数字)
解:由题意知:∠A=30°,∠ACB=90°,∠CBD=30°,AB=80
∴ .
.
在Rt△BCD中,cos∠CBD= ,
,
∴BD=BC•cos30°
=
答:两座楼房的底部BD之间的距离约34.6米.
分析:根据题目已知条件明确有关直角三角形的度数,作CE⊥AB于E,分别求得AE与BE的长,加在一起即为AB的长.
点评:本题考查了解直角三角形中的仰俯角问题,解决此类题目的关键是弄清有关的直角三角形中的有关角的度数.
∴
 .
.在Rt△BCD中,cos∠CBD=
 ,
,∴BD=BC•cos30°
=

答:两座楼房的底部BD之间的距离约34.6米.
分析:根据题目已知条件明确有关直角三角形的度数,作CE⊥AB于E,分别求得AE与BE的长,加在一起即为AB的长.
点评:本题考查了解直角三角形中的仰俯角问题,解决此类题目的关键是弄清有关的直角三角形中的有关角的度数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
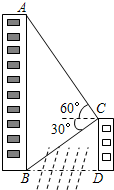 如图,某条河的两岸建有两座楼房.已知写字楼AB的高为80米,小明站在河对岸的一座办公楼CD的楼顶C点处,测得写字楼的楼顶A点处的仰角为60°,测得楼底B点处的俯角为30°.求两座楼房的底部BD之间的距离.
如图,某条河的两岸建有两座楼房.已知写字楼AB的高为80米,小明站在河对岸的一座办公楼CD的楼顶C点处,测得写字楼的楼顶A点处的仰角为60°,测得楼底B点处的俯角为30°.求两座楼房的底部BD之间的距离. ,计算结果保留3个有效数字)
,计算结果保留3个有效数字)